Combine like terms: -4x^3 - 6y^3 + y^3 - 3 + x^3 + x^3 + 4y^3.
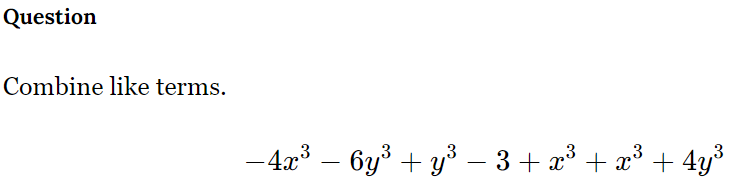
Understand the Problem
The question is asking to combine similar algebraic terms in the expression provided.
Answer
$$ -2x^3 - y^3 - 3 $$
Answer for screen readers
The combined expression is: $$ -2x^3 - y^3 - 3 $$
Steps to Solve
- Identify like terms
In the expression, find the terms with the same variable raised to the same power. Here, we have three types of terms: those containing $x^3$, those containing $y^3$, and the constant.
- Combine the $x^3$ terms
The $x^3$ terms in the expression are: $$ -4x^3 + x^3 + x^3 $$ First, add the coefficients: $$ -4 + 1 + 1 = -2 $$ So, the combined $x^3$ terms give us: $$ -2x^3 $$
- Combine the $y^3$ terms
Next, we look at the $y^3$ terms: $$ -6y^3 + y^3 + 4y^3 $$ Again, add the coefficients: $$ -6 + 1 + 4 = -1 $$ Thus, the combined $y^3$ terms result in: $$ -1y^3 $$
- Combine the constant term
The only constant term in the expression is $-3$. This remains as is since there are no other constants to combine it with.
- Write the final expression
Now that we have combined all the like terms, we can write the final result as: $$ -2x^3 - y^3 - 3 $$
The combined expression is: $$ -2x^3 - y^3 - 3 $$
More Information
Combining like terms is a fundamental skill in algebra, making expressions simpler and easier to work with. In this case, we grouped similar variable terms to form a more concise expression.
Tips
- Ignoring constants: Often, students forget to include constant terms when combining or simplifying expressions.
- Misadding coefficients: Adding coefficients incorrectly, especially with negative numbers, can lead to wrong results.