Combine like terms: -3x^3 + 1 + 4x^3 - 3y^3 - 1 + 5x^3 - 7
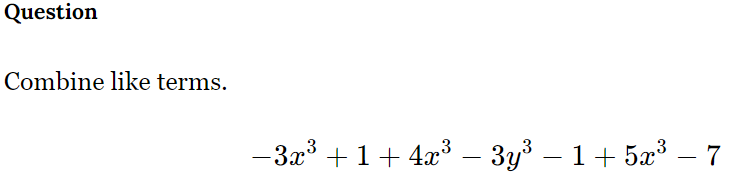
Understand the Problem
The question is asking us to combine like terms from the given polynomial expression. This will involve adding and subtracting the coefficients of terms with the same variable and exponent.
Answer
The simplified expression is \( 6x^3 - 7 \).
Answer for screen readers
The simplified expression is ( 6x^3 - 7 ).
Steps to Solve
-
Identify Like Terms Identify the terms in the expression that have the same variable and exponent. In this case, the like terms are the coefficients of $x^3$ and the constant terms.
-
Combine the $x^3$ Terms The $x^3$ terms are $-3x^3$, $4x^3$, and $5x^3$. We will add these coefficients together: $$ -3 + 4 + 5 $$
Simplifying gives: $$ -3 + 4 = 1 $$ $$ 1 + 5 = 6 $$ So, $-3x^3 + 4x^3 + 5x^3 = 6x^3$.
- Combine the Constant Terms The constant terms are $1$, $-1$, and $-7$. We will add these together: $$ 1 - 1 - 7 $$
Simplifying gives: $$ 1 - 1 = 0 $$ $$ 0 - 7 = -7 $$ So, $1 - 1 - 7 = -7$.
- Combine All Results Now we will combine the simplified $x^3$ terms and the constant term: $$ 6x^3 - 7 $$
The simplified expression is ( 6x^3 - 7 ).
More Information
Combining like terms is essential in polynomial expressions, as it simplifies the expression, making it easier to work with. This process is important in algebra, especially when solving equations or performing operations on polynomials.
Tips
- Forgetting to include all like terms can lead to an incorrect final answer.
- Miscalculating when adding or subtracting coefficients might also occur. Always double-check arithmetic.