Combine like terms: -1 + 4x^3 - 6 + 7y^2 + 5 + 6x^3 - 4x^3
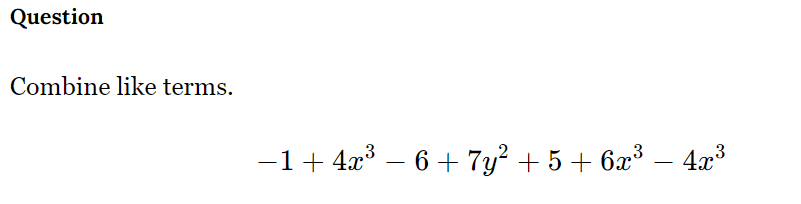
Understand the Problem
The question is asking to combine like terms in the given algebraic expression. This involves identifying and adding or subtracting coefficients of terms that have the same variables raised to the same powers.
Answer
The simplified expression is $6x^3 + 7y^2 - 2$.
Answer for screen readers
The simplified expression is: $$ 6x^3 + 7y^2 - 2 $$
Steps to Solve
- Identify Like Terms
Look at the expression: $$ -1 + 4x^3 - 6 + 7y^2 + 5 + 6x^3 - 4x^3 $$
Group the like terms together:
- Constant terms: $-1, -6, 5$
- $x^3$ terms: $4x^3, 6x^3, -4x^3$
- $y^2$ term: $7y^2$
- Combine Constant Terms
Add the constant terms together: $$ -1 - 6 + 5 $$
Calculating this gives: $$ -1 - 6 = -7 $$ $$ -7 + 5 = -2 $$
So, the combined constant terms result in $-2$.
- Combine x³ Terms
Now, combine the $x^3$ terms: $$ 4x^3 + 6x^3 - 4x^3 $$
Calculating this gives: $$ 4 + 6 - 4 = 6 $$
Thus, the combined $x^3$ terms result in $6x^3$.
- Combine y² Terms
Since there is only one $y^2$ term: $$ 7y^2 $$
This term remains unchanged.
- Write the Simplified Expression
Combine all results from previous steps: $$ -2 + 6x^3 + 7y^2 $$
The simplified expression is: $$ 6x^3 + 7y^2 - 2 $$
More Information
Combining like terms is a fundamental skill in algebra that allows for simplifying expressions. It makes calculations easier and clearer, especially when dealing with complex expressions.
Tips
- Forgetting to change the signs when adding or subtracting terms.
- Mixing different variables when combining terms; only like terms can be combined.
AI-generated content may contain errors. Please verify critical information