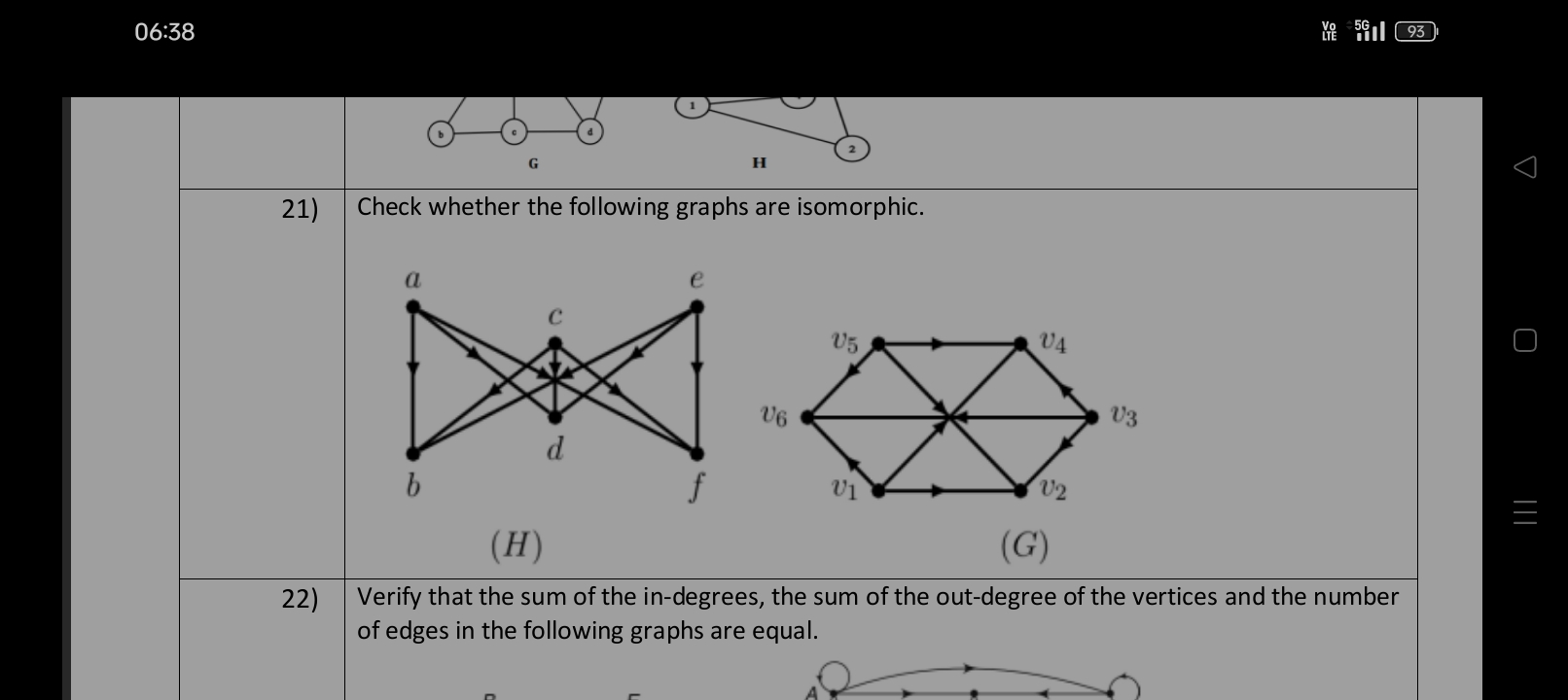
Check whether the following graphs are isomorphic. Verify that the sum of the in-degrees, the sum of the out-degree of the vertices, and the number of edges in the following graphs... Check whether the following graphs are isomorphic. Verify that the sum of the in-degrees, the sum of the out-degree of the vertices, and the number of edges in the following graphs are equal. Read more

Steps to Solve

1. Count the vertices and edges of each graph

For graph (H):

• Vertices: $a, b, c, d, e, f$ (6 vertices)
• Edges: Count the edges between vertices. For example, $a \leftrightarrow b$, $a \leftrightarrow c$, etc.

For graph (G):

• Vertices: $v_1, v_2, v_3, v_4, v_5, v_6$ (6 vertices)
• Edges: Similarly count the edges.

2. Determine degree of each vertex

Calculate the degree for each vertex in both graphs:

• For graph (H), list degrees:

  • $\text{deg}(a), \text{deg}(b), \text{deg}(c), \text{deg}(d), \text{deg}(e), \text{deg}(f)$

• For graph (G), list degrees:

  • $\text{deg}(v_1), \text{deg}(v_2), \text{deg}(v_3), \text{deg}(v_4), \text{deg}(v_5), \text{deg}(v_6)$

3. Create a degree sequence

List the degree sequences:

• Graph (H): Sort the list of degrees in descending order.
• Graph (G): Sort the list of degrees in descending order.

4. Compare degree sequences

Check if the degree sequences for both graphs are identical. If they are, it suggests the graphs could be isomorphic.

5. Check for one-to-one correspondence

If the degree sequences match, construct a mapping of vertices from graph (H) to graph (G) to see if edges correspond.

6. Verify in-degrees and out-degrees

For part 22:

• In-degrees: Count how many edges point to each vertex in both graphs.
• Out-degrees: Count how many edges originate from each vertex.
• Compute the total in-degrees and out-degrees and verify if they match the number of edges.

7. Sum the in-degrees and out-degrees

Calculate the sums:

• Sum of in-degrees for both graphs.
• Sum of out-degrees for both graphs.
• Ensure the sums equal the number of edges.