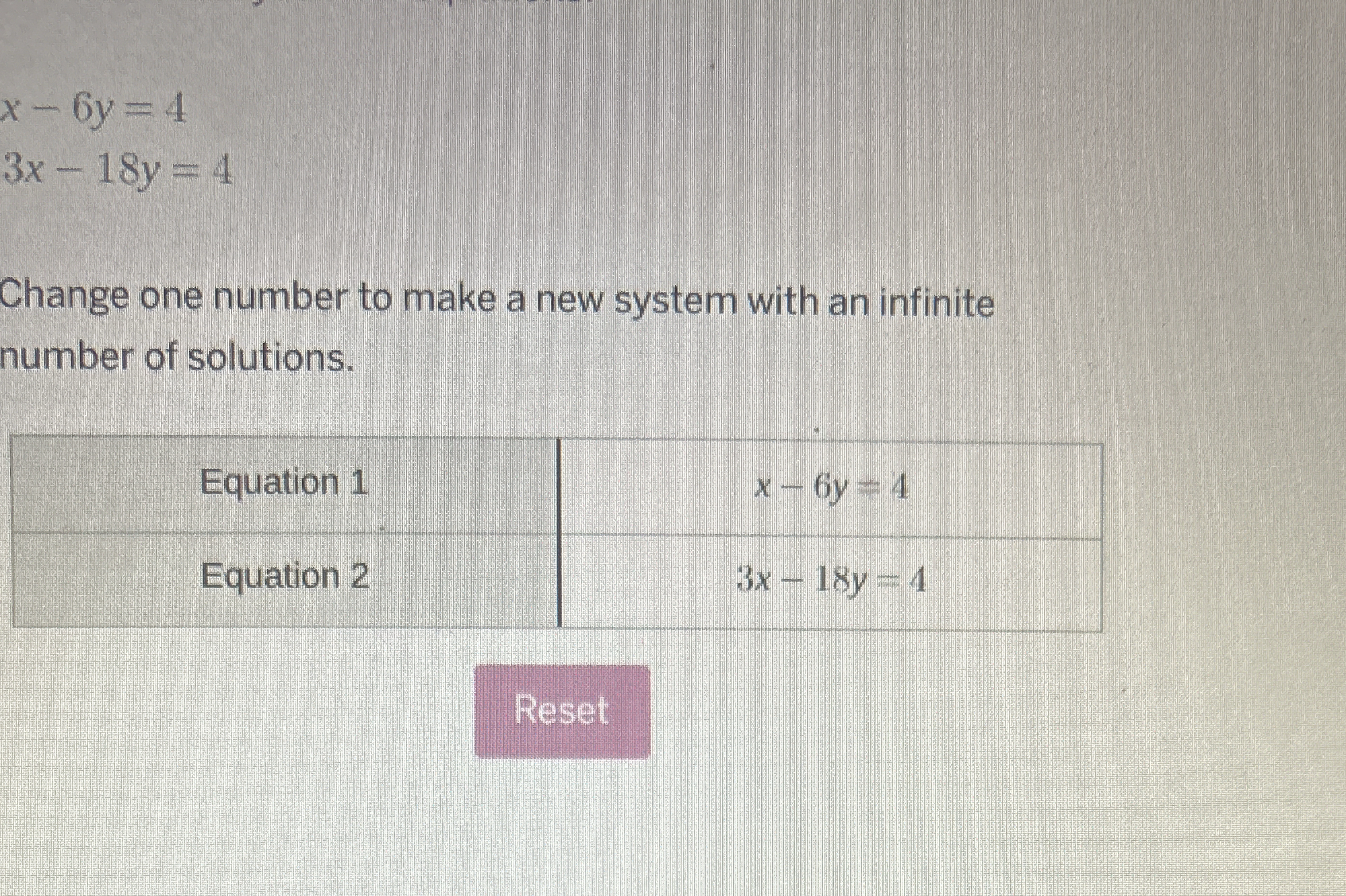
Change one number to make a new system with an infinite number of solutions.
Understand the Problem
The question is asking how to modify one of the given equations in such a way that the two equations become dependent, resulting in an infinite number of solutions for the system. This typically involves making one equation a multiple of the other.
Answer
Change Equation 2 to $$3x - 18y = 12$$.
Answer for screen readers
To create a new system with an infinite number of solutions, change Equation 2 to: $$ 3x - 18y = 12 $$
Steps to Solve
-
Identify the equations The original equations are: $$ x - 6y = 4 $$ $$ 3x - 18y = 4 $$
-
Determine if they are dependent To make the equations dependent, one equation must be a scalar multiple of the other. We know that if we multiply Equation 1 by 3, we get: $$ 3(x - 6y) = 3(4) $$ This simplifies to: $$ 3x - 18y = 12 $$
-
Change a number in Equation 2 Currently, Equation 2 is: $$ 3x - 18y = 4 $$ To make it dependent on Equation 1, we will change the right-hand side to match the new constant we obtained from Equation 1: $$ 3x - 18y = 12 $$
-
Resulting equations Now the two equations become: $$ x - 6y = 4 $$ $$ 3x - 18y = 12 $$
These are dependent because Equation 2 is now a multiple of Equation 1.
To create a new system with an infinite number of solutions, change Equation 2 to: $$ 3x - 18y = 12 $$
More Information
When two equations represent the same line, they have an infinite number of solutions. This means that any solution to one equation is also a solution to the other.
Tips
- Changing the wrong side of the equation: Make sure to only change the right side to match the expected multiple, not both sides or leave the left side unchanged.
- Assuming linear combinations yield different equations: Remember, only multiplying or adjusting constants can maintain dependency.
AI-generated content may contain errors. Please verify critical information