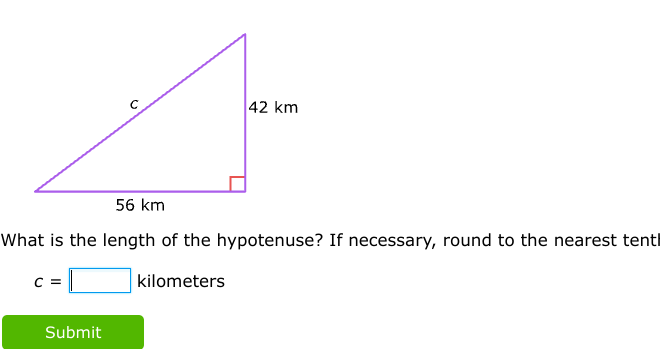
What is the length of the hypotenuse? If necessary, round to the nearest tenth.

Steps to Solve

1. State the Pythagorean Theorem

The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse, $c$, is equal to the sum of the squares of the lengths of the other two sides, $a$ and $b$. This can be expressed as: $$ c^2 = a^2 + b^2 $$

2. Identify the side lengths

In this problem, the lengths of the two sides are given:

• $a = 56 \text{ km}$
• $b = 42 \text{ km}$

3. Substitute the values into the equation

We can substitute the values into the Pythagorean theorem: $$ c^2 = (56)^2 + (42)^2 $$

4. Calculate the squares of the side lengths

Now we calculate: $$ (56)^2 = 3136 $$ $$ (42)^2 = 1764 $$

5. Add the squares

Combine the squares to find $c^2$: $$ c^2 = 3136 + 1764 = 4900 $$