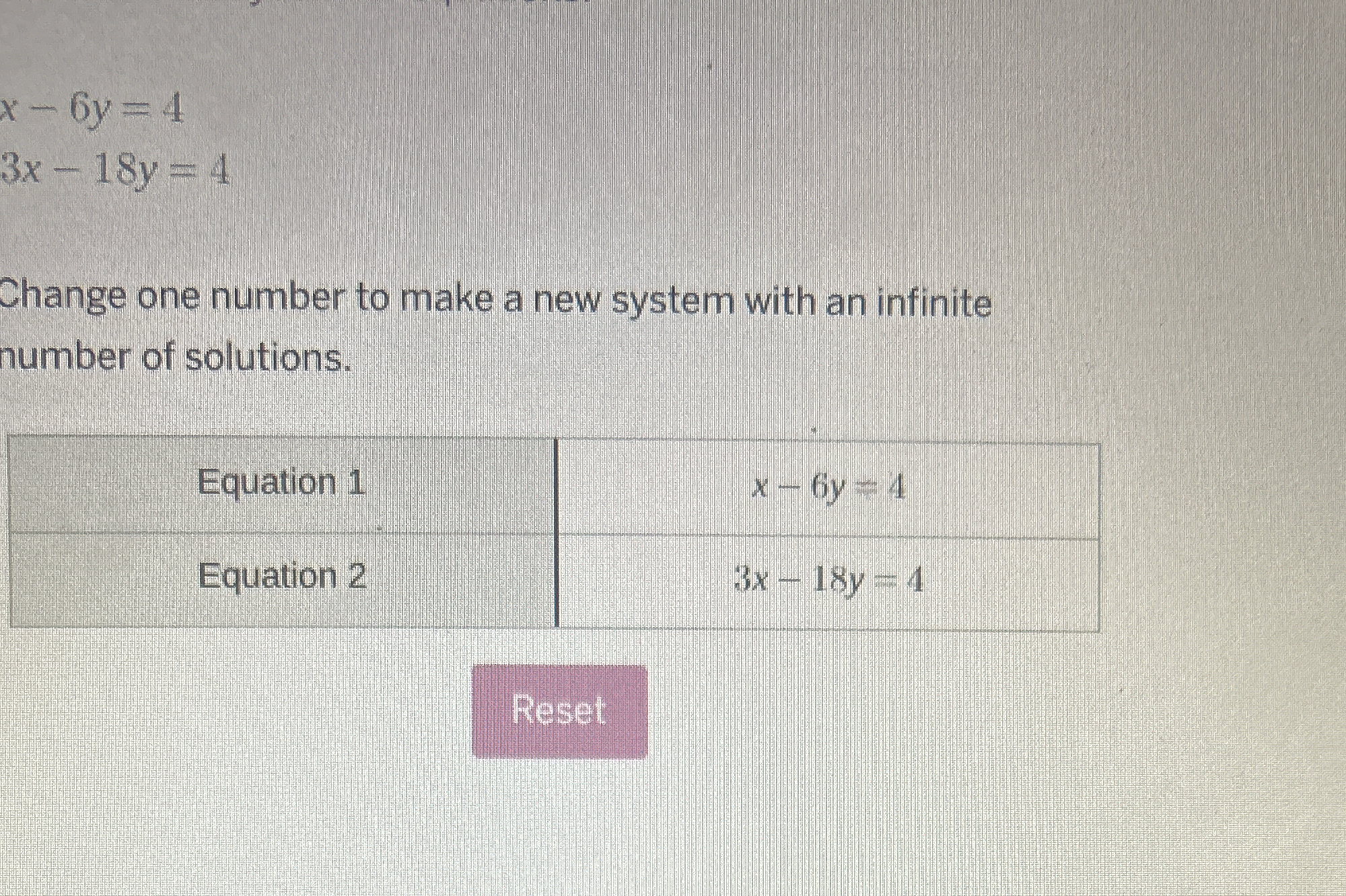
Change one number to make a new system with an infinite number of solutions.

Steps to Solve

1. Identify the Equations We have the following system of equations: $$ \text{Equation 1:} \quad x - 6y = 4 $$ $$ \text{Equation 2:} \quad 3x - 18y = 4 $$

2. Determine the Condition for Infinite Solutions For a system of equations to have an infinite number of solutions, the two equations must be multiples of each other. This means that the ratios of corresponding coefficients must be equal.

3. Check the Ratios of Coefficients From Equation 1, we can express the coefficients:

• Coefficient of $x$: 1 (from Equation 1) and 3 (from Equation 2)
• Coefficient of $y$: -6 (from Equation 1) and -18 (from Equation 2)

We can check the ratio: $$ \frac{1}{3} \quad \text{and} \quad \frac{-6}{-18} = \frac{1}{3} $$ Since the ratios are the same, we can make a change in Equation 2 to maintain this relationship.

4. Choose a New Value for the Constant To maintain the infinite solutions while changing one number, we need to set the constant in Equation 2 to match the scaled-down version of the first equation.

Using a scalar of 3: $$ 3(x - 6y = 4) \quad \Rightarrow \quad 3x - 18y = 12 $$

5. Change Equation 2 Change the constant in Equation 2 from 4 to 12: $$ \text{New Equation 2:} \quad 3x - 18y = 12 $$