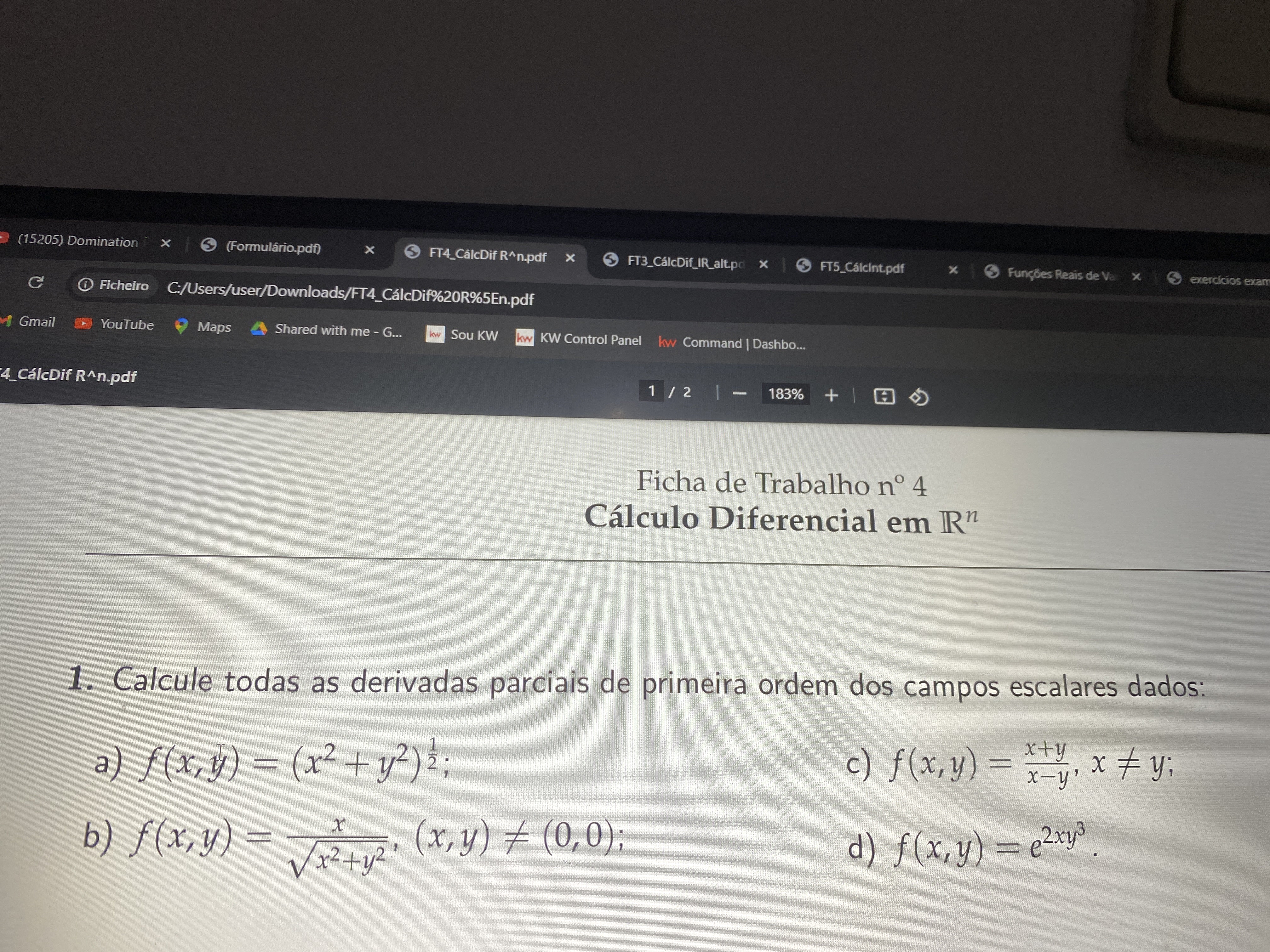
Calcule todas as derivadas parciais de primeira ordem dos campos escalares dados: a) f(x,y) = (x² + y²)^(1/2); b) f(x,y) = x / √(x² + y²), (x,y) ≠ (0,0); c) f(x,y) = (x + y) / (... Calcule todas as derivadas parciais de primeira ordem dos campos escalares dados: a) f(x,y) = (x² + y²)^(1/2); b) f(x,y) = x / √(x² + y²), (x,y) ≠ (0,0); c) f(x,y) = (x + y) / (x - y), x ≠ y; d) f(x,y) = e^(2xy³).
Understand the Problem
A pergunta solicita o cálculo de todas as derivadas parciais de primeira ordem para funções dadas. O problema envolve o uso de regras de diferenciação em várias funções de duas variáveis.
Answer
a) $f_x(x,y) = \frac{x}{(x^2 + y^2)^{1/2}}$, $f_y(x,y) = \frac{y}{(x^2 + y^2)^{1/2}}$ b) $f_x(x,y) = \frac{y^2}{(x^2 + y^2)^{3/2}}$, $f_y(x,y) = \frac{-xy}{(x^2 + y^2)^{3/2}}$ c) $f_x(x,y) = \frac{-2y}{(x - y)^2}$, $f_y(x,y) = \frac{2x}{(x - y)^2}$ d) $f_x(x,y) = 2y^3 e^{2xy^3}$, $f_y(x,y) = 6xy^2 e^{2xy^3}$
Answer for screen readers
a) $f_x(x,y) = \frac{x}{(x^2 + y^2)^{1/2}}, ; f_y(x,y) = \frac{y}{(x^2 + y^2)^{1/2}}$
b) $f_x(x,y) = \frac{y^2}{(x^2 + y^2)^{3/2}}, ; f_y(x,y) = \frac{-xy}{(x^2 + y^2)^{3/2}}$
c) $f_x(x,y) = \frac{-2y}{(x - y)^2}, ; f_y(x,y) = \frac{2x}{(x - y)^2}$
d) $f_x(x,y) = 2y^3 e^{2xy^3}, ; f_y(x,y) = 6xy^2 e^{2xy^3}$
Steps to Solve
- Derivada parcial de f(x,y) = (x² + y²)^(1/2)
Para encontrar as derivadas parciais de $f(x,y) = (x^2 + y^2)^{1/2}$, utilizamos a regra da cadeia.
A derivada parcial em relação a $x$ é: $$ f_x(x,y) = \frac{\partial}{\partial x}(x^2 + y^2)^{1/2} = \frac{x}{(x^2 + y^2)^{1/2}} $$
A derivada parcial em relação a $y$ é: $$ f_y(x,y) = \frac{\partial}{\partial y}(x^2 + y^2)^{1/2} = \frac{y}{(x^2 + y^2)^{1/2}} $$
- Derivada parcial de f(x,y) = x / √(x² + y²)
Para a função $f(x,y) = \frac{x}{(x^2 + y^2)^{1/2}}$, utilizamos a regra do quociente.
A derivada parcial em relação a $x$ é: $$ f_x(x,y) = \frac{(x^2 + y^2)^{1/2} \cdot 1 - x \cdot \frac{1}{2}(x^2 + y^2)^{-1/2} \cdot 2x}{(x^2 + y^2)} = \frac{y^2}{(x^2 + y^2)^{3/2}} $$
A derivada parcial em relação a $y$ é: $$ f_y(x,y) = \frac{-x \cdot \frac{1}{2}(x^2 + y^2)^{-1/2} \cdot 2y}{(x^2 + y^2)} = \frac{-xy}{(x^2 + y^2)^{3/2}} $$
- Derivada parcial de f(x,y) = (x + y) / (x - y)
Para a função $f(x,y) = \frac{x+y}{x-y}$, aplicamos a regra do quociente.
A derivada parcial em relação a $x$ é: $$ f_x(x,y) = \frac{(x-y)(1) - (x+y)(1)}{(x-y)^2} = \frac{-2y}{(x - y)^2} $$
A derivada parcial em relação a $y$ é: $$ f_y(x,y) = \frac{(x-y)(1) - (x+y)(-1)}{(x-y)^2} = \frac{2x}{(x - y)^2} $$
- Derivada parcial de f(x,y) = e^(2xy³)
Para a função $f(x,y) = e^{2xy^3}$, utilizamos a regra da cadeia.
A derivada parcial em relação a $x$ é: $$ f_x(x,y) = e^{2xy^3} \cdot (2y^3) $$
A derivada parcial em relação a $y$ é: $$ f_y(x,y) = e^{2xy^3} \cdot (6xy^2) $$
a) $f_x(x,y) = \frac{x}{(x^2 + y^2)^{1/2}}, ; f_y(x,y) = \frac{y}{(x^2 + y^2)^{1/2}}$
b) $f_x(x,y) = \frac{y^2}{(x^2 + y^2)^{3/2}}, ; f_y(x,y) = \frac{-xy}{(x^2 + y^2)^{3/2}}$
c) $f_x(x,y) = \frac{-2y}{(x - y)^2}, ; f_y(x,y) = \frac{2x}{(x - y)^2}$
d) $f_x(x,y) = 2y^3 e^{2xy^3}, ; f_y(x,y) = 6xy^2 e^{2xy^3}$
More Information
As derivadas parciais fornecem informações sobre como uma função muda em relação a uma variável enquanto mantém as outras constantes. Elas são essenciais em otimização, física e em várias aplicações em engenharia.
Tips
- Não aplicar corretamente a regra da cadeia.
- Esquecer de simplificar as expressões.
- Misturar as variáveis durante o cálculo das derivadas.
AI-generated content may contain errors. Please verify critical information