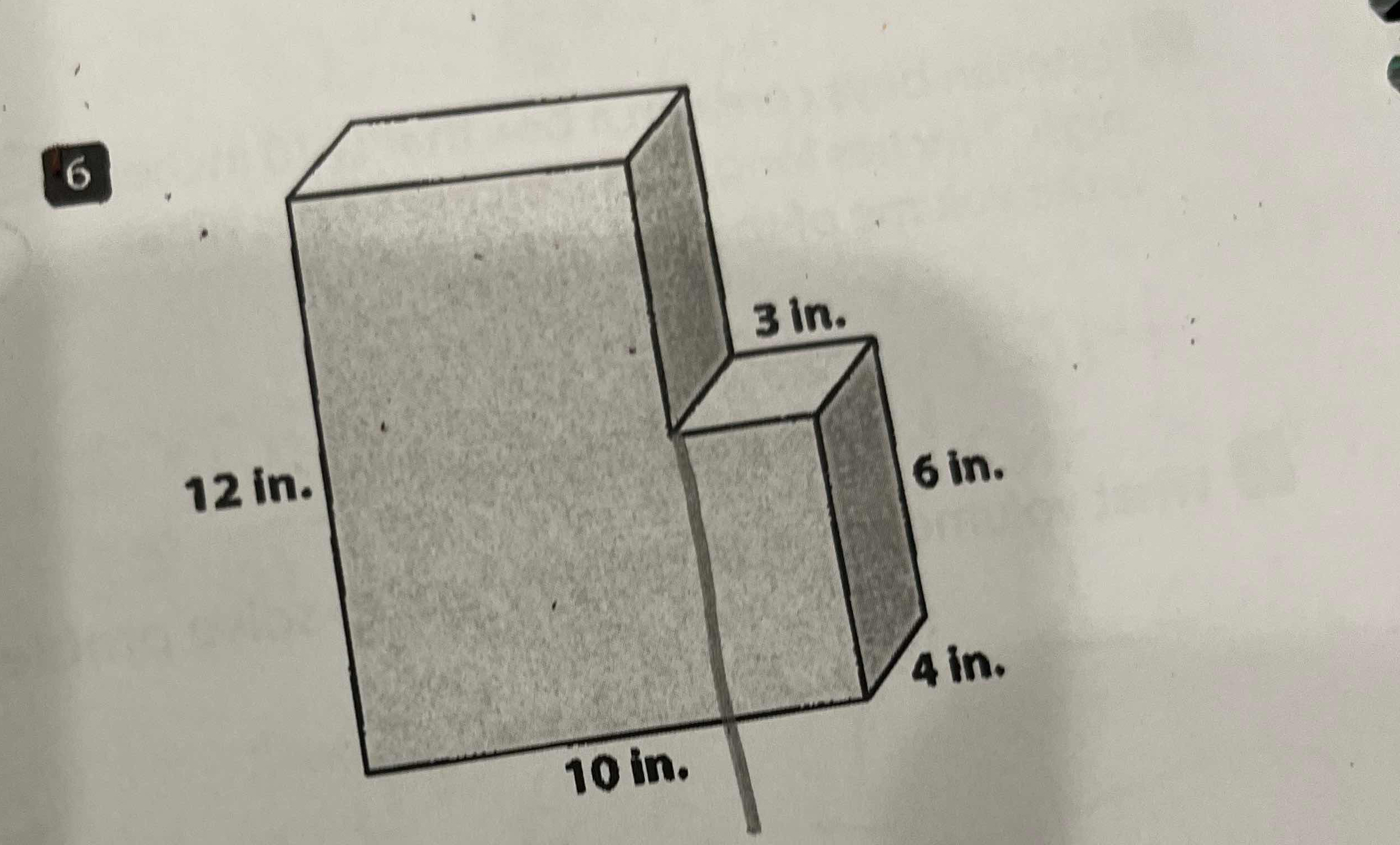
Calculate the volume of the composite shape shown in the image.
Understand the Problem
The question involves calculating the volume of a composite shape composed of two rectangular prisms. The dimensions provided suggest we need to use the volume formula for rectangles (length × width × height) for each of the two prisms and then combine the results.
Answer
The total volume is \( 360 \, \text{in}^3 \).
Answer for screen readers
The total volume of the composite shape is ( V = 360 , \text{in}^3 ).
Steps to Solve
- Identify Dimensions of the First Prism
The first prism has dimensions:
- Length = 10 in
- Width = 12 in
- Height = 3 in
- Calculate Volume of the First Prism
Use the volume formula for a rectangular prism:
[ \text{Volume} = \text{Length} \times \text{Width} \times \text{Height} ]
For the first prism:
[ V_1 = 10 , \text{in} \times 12 , \text{in} \times 3 , \text{in} ]
- Identify Dimensions of the Second Prism
The second prism has dimensions:
- Length = 6 in
- Width = 4 in
- Height = 12 in
- Calculate Volume of the Second Prism
Using the same volume formula:
[ V_2 = 6 , \text{in} \times 4 , \text{in} \times 12 , \text{in} ]
- Combine the Volumes
To find the total volume of the composite shape, add the volume of both prisms:
[ \text{Total Volume} = V_1 + V_2 ]
The total volume of the composite shape is ( V = 360 , \text{in}^3 ).
More Information
The calculation involves finding the volume of each rectangular prism separately and then summing them. The volume formula for rectangular prisms is a fundamental concept in geometry.
Tips
- Forgetting to multiply all three dimensions when calculating the volume.
- Confusing dimensions between the two prisms.
- Incorrectly summing the volumes (wrong arithmetic).
AI-generated content may contain errors. Please verify critical information