Calculate the volume of a stacked rectangular prism structure with given dimensions.
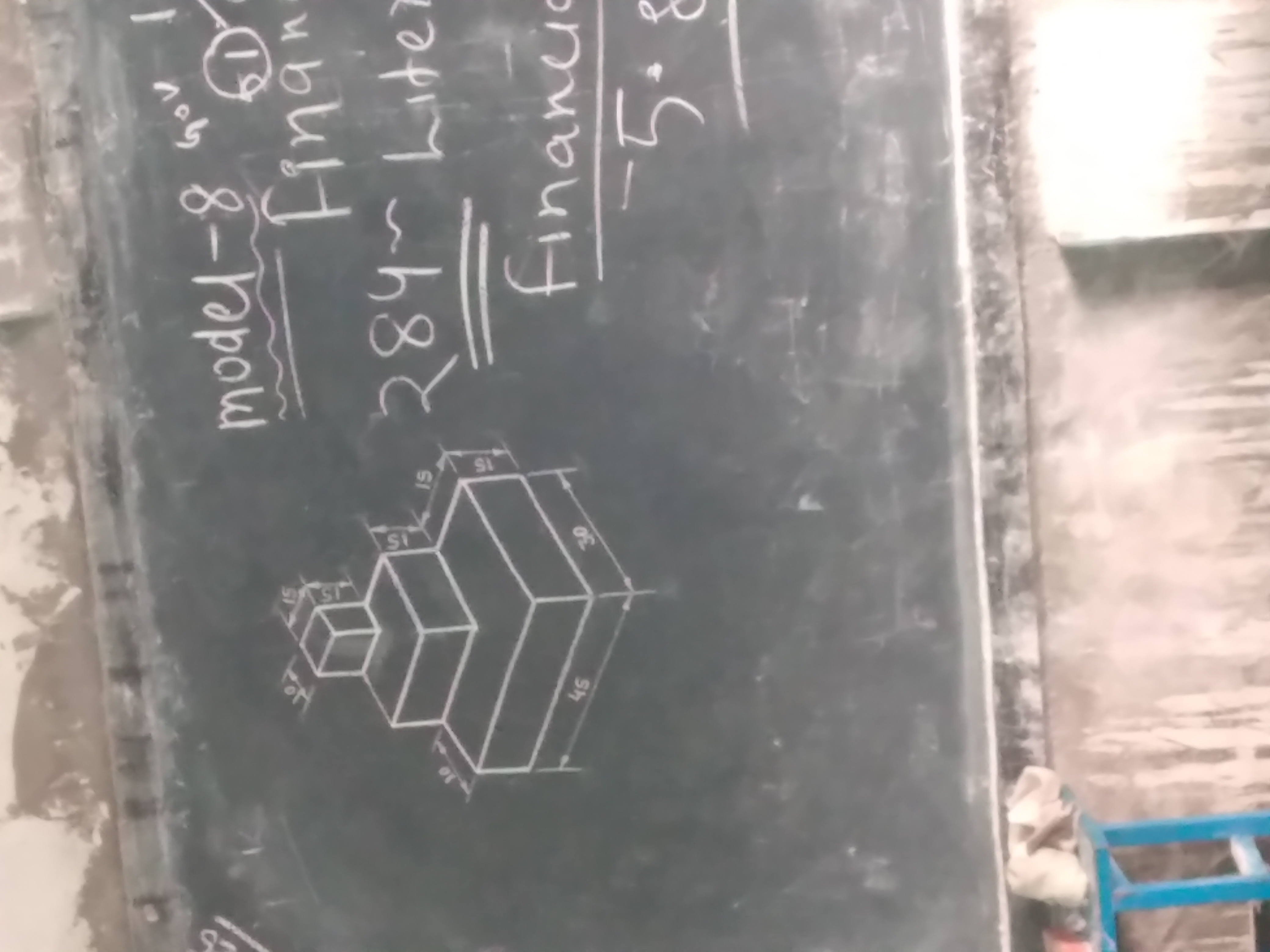
Understand the Problem
The question involves calculating the volume of a three-dimensional shape made up of stacked rectangular prisms. It seems to require identifying dimensions and potentially applying a formula for volume based on the given measurements.
Answer
The total volume of the stacked rectangular prisms is $31500 \text{ cm}^3$.
Answer for screen readers
The total volume of the stacked rectangular prisms is $31500 \text{ cm}^3$.
Steps to Solve
-
Identify the dimensions of each rectangular prism The drawing shows a shape made of three stacked rectangular prisms. The dimensions are provided as:
- Bottom prism: Length = 45 cm, Width = 30 cm, Height = 15 cm
- Middle prism: Length = 30 cm, Width = 30 cm, Height = 10 cm
- Top prism: Length = 15 cm, Width = 15 cm, Height = 10 cm
-
Calculate the volume of each prism The volume $V$ of a rectangular prism is given by the formula: $$ V = \text{Length} \times \text{Width} \times \text{Height} $$
-
Bottom prism: $$ V_1 = 45 \times 30 \times 15 $$
-
Middle prism: $$ V_2 = 30 \times 30 \times 10 $$
-
Top prism: $$ V_3 = 15 \times 15 \times 10 $$
-
-
Perform the calculations
-
For the bottom prism: $$ V_1 = 45 \times 30 \times 15 = 20250 \text{ cm}^3 $$
-
For the middle prism: $$ V_2 = 30 \times 30 \times 10 = 9000 \text{ cm}^3 $$
-
For the top prism: $$ V_3 = 15 \times 15 \times 10 = 2250 \text{ cm}^3 $$
-
-
Sum the volumes To find the total volume $V_{total}$, sum the volumes of the three prisms: $$ V_{total} = V_1 + V_2 + V_3 $$ $$ V_{total} = 20250 + 9000 + 2250 $$
-
Final Calculation Calculate the total volume: $$ V_{total} = 20250 + 9000 + 2250 = 31500 \text{ cm}^3 $$
The total volume of the stacked rectangular prisms is $31500 \text{ cm}^3$.
More Information
This problem involves calculating the volume of three rectangular prisms stacked on top of one another. The units are in cubic centimeters, and the final result can also be converted to liters, where $1 \text{ liter} = 1000 \text{ cm}^3$. Thus, the total volume in liters would be $31.5 \text{ liters}$.
Tips
- Not using the correct dimensions for each prism when calculating volume.
- Forgetting to convert volumes to the desired unit (liters) if needed.
AI-generated content may contain errors. Please verify critical information