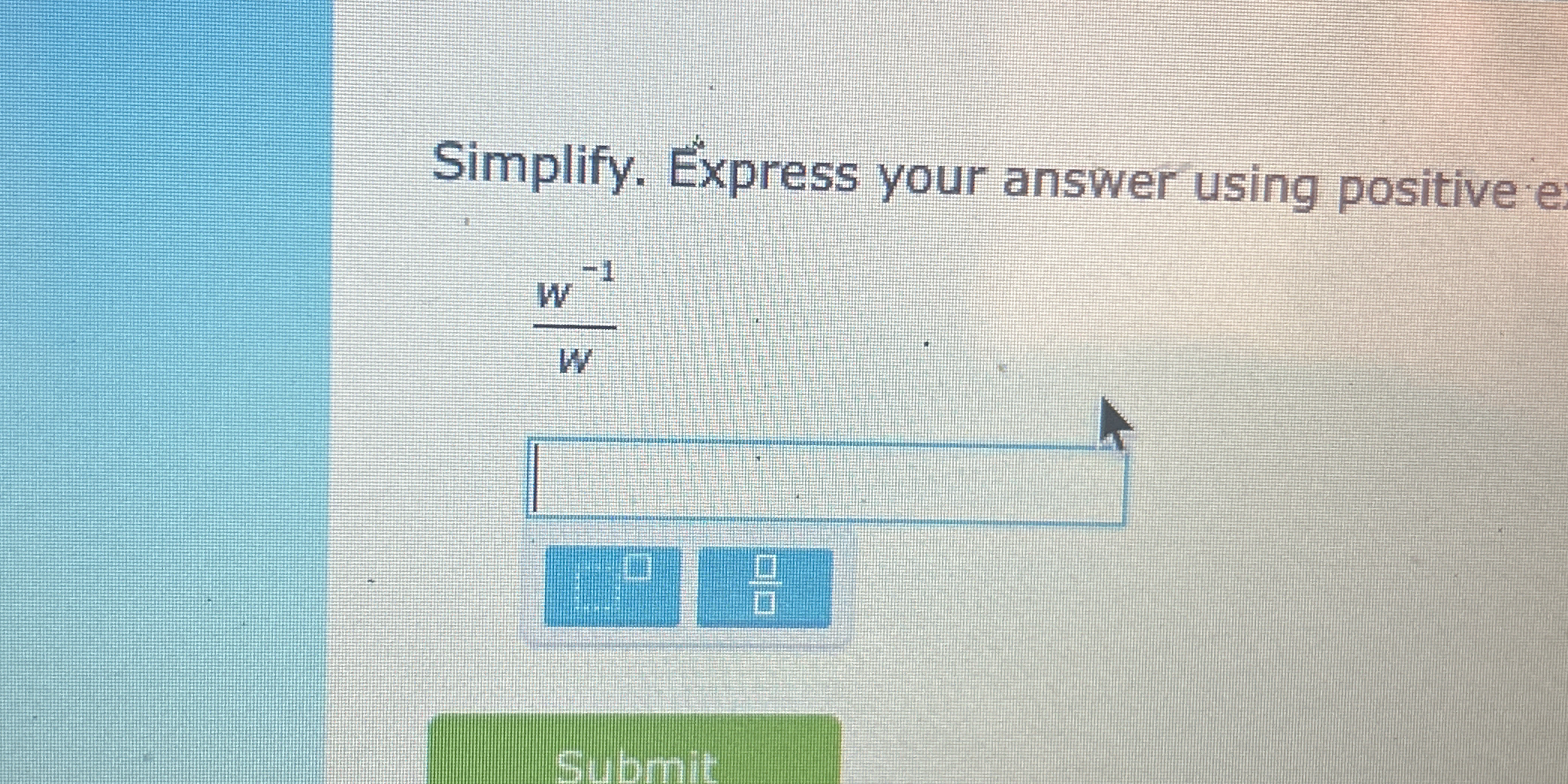
Simplify \( \frac{w^{-1}}{w} \) and express your answer using positive exponents.
Understand the Problem
The question asks to simplify the expression ( \frac{w^{-1}}{w} ) and express the answer using positive exponents. This requires understanding of exponent rules, particularly dealing with negative exponents.
Answer
The simplified expression is \( \frac{1}{w^2} \).
Answer for screen readers
The simplified expression is ( \frac{1}{w^2} ).
Steps to Solve
-
Identify the expression to simplify We start with the expression ( \frac{w^{-1}}{w} ).
-
Apply the laws of exponents Using the rule ( \frac{a^m}{a^n} = a^{m-n} ), we can rewrite the expression as follows: $$ \frac{w^{-1}}{w} = w^{-1 - 1} = w^{-2} $$
-
Convert to positive exponent To express ( w^{-2} ) using positive exponents, we use the rule ( a^{-n} = \frac{1}{a^n} ): $$ w^{-2} = \frac{1}{w^2} $$
The simplified expression is ( \frac{1}{w^2} ).
More Information
Simplifying expressions with negative exponents is a common practice in algebra. It helps in making expressions easier to read and work with. This particular example highlights the conversion from a negative to a positive exponent.
Tips
- Confusing the subtraction in the exponent rule, which may lead to incorrect simplification such as ( w^{-2} ) being written as ( w^2 ) instead.
- Forgetting to convert negative exponents into their positive form.
AI-generated content may contain errors. Please verify critical information