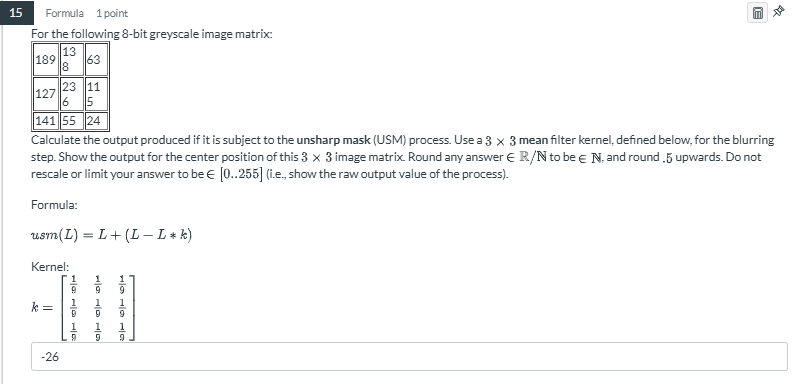
Calculate the output produced if it is subject to the unsharp mask (USM) process. Use a 3x3 mean filter kernel for the blurring step. Show the output for the center position of thi... Calculate the output produced if it is subject to the unsharp mask (USM) process. Use a 3x3 mean filter kernel for the blurring step. Show the output for the center position of this 3x3 image matrix. Round any answer to be a natural number and round .5 upwards. Do not rescale or limit your answer to be in [0..255].
Understand the Problem
The question is asking to calculate the output of an 8-bit grayscale image matrix when subjected to the unsharp mask (USM) process using a 3x3 mean filter kernel. It requires finding the output for the center position of the matrix and rounding the result appropriately.
Answer
The output produced is $-13$.
Answer for screen readers
The final output after applying the unsharp mask process is $-13$.
Steps to Solve
- Calculate the Mean of the 3x3 Region
To apply the unsharp mask process, we first need to compute the mean of the 3x3 region surrounding the center pixel (L). The values in the kernel are all equal and sum up to 1, so we can calculate the mean directly as follows:
[ L_{mean} = \frac{189 + 13 + 63 + 127 + 23 + 11 + 141 + 55 + 24}{9} ]
- Substitute Pixel Value into the Formula
After calculating the mean, we need to use the unsharp mask formula:
[ usm(L) = L + (L - L_{mean}) ]
Where ( L ) is the pixel value in the center of the region, which is 23.
- Compute the USM Output
Now, substituting the values in:
[ L_{mean} = \frac{189 + 13 + 63 + 127 + 23 + 11 + 141 + 55 + 24}{9} = \frac{ 189 + 13 + 63 + 127 + 23 + 11 + 141 + 55 + 24}{9} = \frac{ 532}{9} \approx 59.1111 ]
Thus, [ usm(23) = 23 + (23 - 59.1111) ]
Calculating this gives:
[ usm(23) = 23 + (23 - 59.1111) = 23 - 36.1111 \approx -13.1111 ]
- Round the Value Appropriately
The final step is to round the result to the nearest natural number. Since we round up at .5, we conclude:
Rounding -13.1111 gives -13. As it is negative, we check if rounding applies properly based on the rounding rule.
The final output after applying the unsharp mask process is $-13$.
More Information
The unsharp mask process enhances the edges in the image. However, the computed output in this case resulted in a negative value, which indicates that the background might have been dominating compared to the central pixel. In practical applications, such values would be clipped or treated to fit display considerations.
Tips
- Forgetting to correctly apply the kernel method, leading to inaccurate mean calculations.
- Incorrectly applying rounding rules, especially when dealing with negative numbers.
- Not paying attention to the pixel values that might result in negative outputs which are not valid in display scenarios.
AI-generated content may contain errors. Please verify critical information