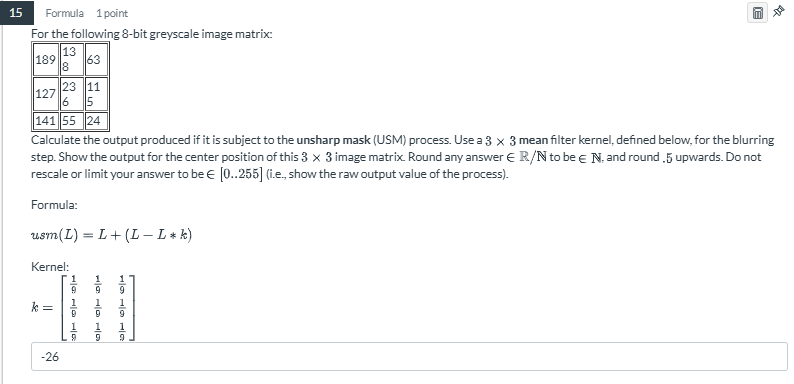
Calculate the output produced if it is subject to the unsharp mask (USM) process. Use a 3 x 3 mean filter kernel for the blurring step. Show the output for the center position of t... Calculate the output produced if it is subject to the unsharp mask (USM) process. Use a 3 x 3 mean filter kernel for the blurring step. Show the output for the center position of this 3 x 3 image matrix. Round any answer to be a natural number and round .5 upwards. Do not rescale or limit your answer to be in the range [0, 255].
Understand the Problem
The question is asking us to calculate the output of an 8-bit grayscale image matrix when subjected to the unsharp mask (USM) process using a 3x3 mean filter kernel. Specifically, we need to apply the formula given and round the results accordingly for the center position of the specified matrix. This involves performing matrix operations as defined by the USM formula.
Answer
The output value produced by the USM process is $1$.
Answer for screen readers
The final output of the unsharp mask process for the center pixel is $1$.
Steps to Solve
-
Extract the Center Pixel
Identify the 3x3 matrix around the center pixel of the given grayscale image matrix for calculation. The center pixel is located at (2, 1), which corresponds to the value 5. The 3x3 matrix looks like this: $$ \begin{bmatrix} 23 & 11 & 63 \ 55 & 5 & 24 \ 141 & 55 & 24 \end{bmatrix} $$
-
Calculate the Mean of the Surrounding Pixels
Calculate the mean (average) of the pixel values in the 3x3 matrix. The sum of the pixels is: $$ 23 + 11 + 63 + 55 + 5 + 24 + 141 + 55 + 24 = 367 $$ The total number of pixels is 9, so the mean is: $$ \text{mean} = \frac{367}{9} \approx 40.78 $$
-
Apply the Unsharp Mask Formula
Using the unsharp mask formula given: $$ \text{usm}(L) = L + (L - \text{mean}) * k $$ Here, ( L ) is the center pixel (5) and ( k ) is the kernel coefficient, which is ( \frac{1}{9} ). We need to calculate: $$ \text{usm}(5) = 5 + (5 - 40.78) * \frac{1}{9} $$
-
Calculate the Final Output
Now, substituting the values into the equation: $$ (5 - 40.78) = -35.78 $$ Multiply by ( \frac{1}{9} ): $$ \frac{-35.78}{9} \approx -3.9756 $$ Therefore, $$ \text{usm}(5) = 5 + (-3.9756) \approx 1.0244 $$
Rounding this to the nearest integer from below: $$ \text{Final output} = 1 $$
The final output of the unsharp mask process for the center pixel is $1$.
More Information
The unsharp mask process emphasizes image details by subtracting a blurred version of the image, effectively enhancing sharpness. Here we calculated the mean of the surrounding pixels to determine how much detail to enhance.
Tips
- Incorrectly calculating the mean: Ensure all relevant pixel values are summed accurately.
- Forgetting to round correctly: Remember to round the final value according to the specified rules (to the nearest integer or specified rounding method).
- Misapplying the formula: Make sure to substitute values in the correct order and check the arithmetic.
AI-generated content may contain errors. Please verify critical information