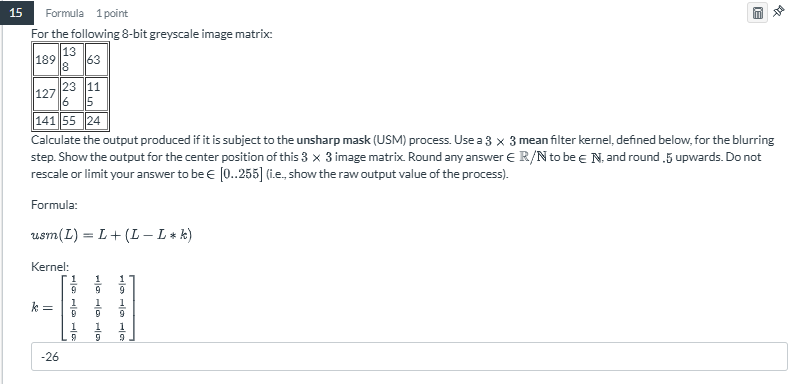
Calculate the output produced if it is subject to the unsharp mask (USM) process. Use a 3 x 3 mean filter kernel. Show the output for the center position of this 3 x 3 image matrix... Calculate the output produced if it is subject to the unsharp mask (USM) process. Use a 3 x 3 mean filter kernel. Show the output for the center position of this 3 x 3 image matrix. Round any answer to be a natural number and round .5 upwards. Do not rescale or limit your answer to be in the range [0, 255]. Read more

Steps to Solve

1. Extract the Center Pixel Value First, we identify the value of the center pixel in the 3x3 matrix, which we will denote as $L$. From the provided grayscale image matrix:

$$ \begin{bmatrix} 189 & 13 & 63 \ 127 & 23 & 11 \ 141 & 55 & 24 \end{bmatrix} $$

The center pixel is $L = 23$ (position at row 2, column 2).

2. Calculate the Mean with the Kernel Next, we apply the 3x3 mean filter kernel. The kernel is given by:

$$ k = \begin{bmatrix} \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \ \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \ \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \end{bmatrix} $$

Calculating the mean for the 3x3 block:

$$ L_{\text{mean}} = \frac{189 + 13 + 63 + 127 + 23 + 11 + 141 + 55 + 24}{9} = \frac{ 189 + 13 + 63 + 127 + 23 + 11 + 141 + 55 + 24 }{9} = \frac{ 608 }{9} \approx 67.56 $$

3. Apply the Unsharp Mask Formula We now use the unsharp mask (USM) formula:

$$ usm(L) = L + (L - L_{\text{mean}}) $$

Substituting the values we found:

• $L = 23$
• $L_{\text{mean}} \approx 67.56$

Calculating:

$$ usm(L) = 23 + (23 - 67.56) = 23 + ( -44.56 ) \approx -21.56 $$

4. Round the Result According to the problem, we need to round to the nearest natural number, rounding up if we encounter a .5 value. Rounding $-21.56$ gives us:

$$ \text{Rounded Result} = -22 $$