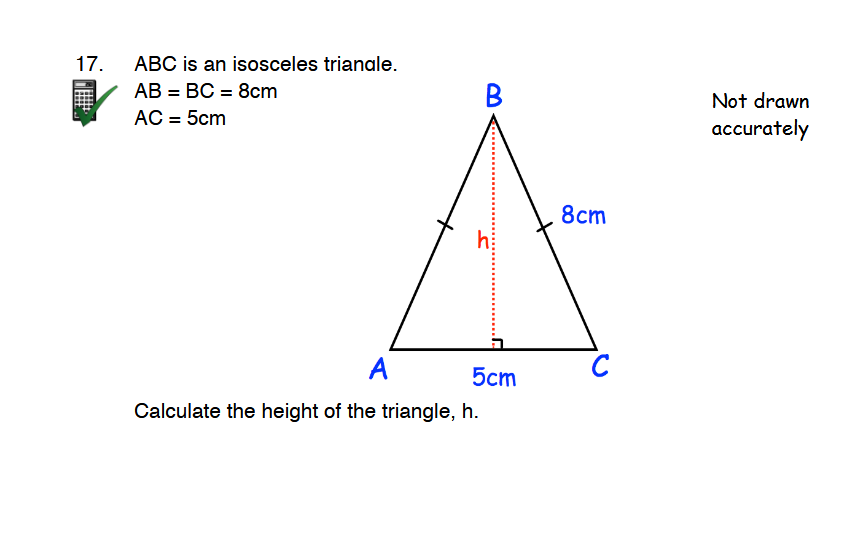
Calculate the height of the triangle, h.
Understand the Problem
The question is asking to calculate the height of an isosceles triangle ABC, where the lengths of the sides are given. To find the height, we can drop a perpendicular from point B to line AC, creating two right triangles. We can use the Pythagorean theorem to solve for the height.
Answer
The height of the triangle is \( h \approx 7.6 \, \text{cm} \).
Answer for screen readers
The height of the triangle, ( h ), is approximately ( h \approx 7.6 , \text{cm} ).
Steps to Solve
-
Identify the triangle properties Since triangle ABC is isosceles, we know that ( AB = BC = 8 , \text{cm} ) and ( AC = 5 , \text{cm} ).
-
Draw the height Drop a perpendicular from point B to side AC, meeting AC at point D. This gives us two right triangles: ABD and BCD. Both triangles are congruent.
-
Calculate the length of AD Since AC is divided into two equal segments by the perpendicular, we have: $$ AD = DC = \frac{AC}{2} = \frac{5}{2} = 2.5 , \text{cm} $$
-
Apply the Pythagorean theorem In triangle ABD, we can use the Pythagorean theorem to find the height ( h ): $$ AB^2 = AD^2 + h^2 $$
Substituting the known values, we have: $$ 8^2 = 2.5^2 + h^2 $$
-
Calculate the squares Calculate the squares: $$ 64 = 6.25 + h^2 $$
-
Isolate h Rearranging the equation gives: $$ h^2 = 64 - 6.25 $$ $$ h^2 = 57.75 $$
-
Solve for h Take the square root: $$ h = \sqrt{57.75} \approx 7.6 , \text{cm} $$
The height of the triangle, ( h ), is approximately ( h \approx 7.6 , \text{cm} ).
More Information
This triangle's height was calculated using the properties of isosceles triangles and the Pythagorean theorem, which relates the lengths of the sides of right triangles. The height is vital for many triangle-related calculations, such as area.
Tips
- Not dividing AC correctly: Ensure to divide the base correctly in an isosceles triangle when dropping a height.
- Squaring errors: Mistakes when squaring numbers or simplifying can lead to incorrect results.
- Forgetting the height: Remember that the height is always the perpendicular distance from a vertex to the base.
AI-generated content may contain errors. Please verify critical information