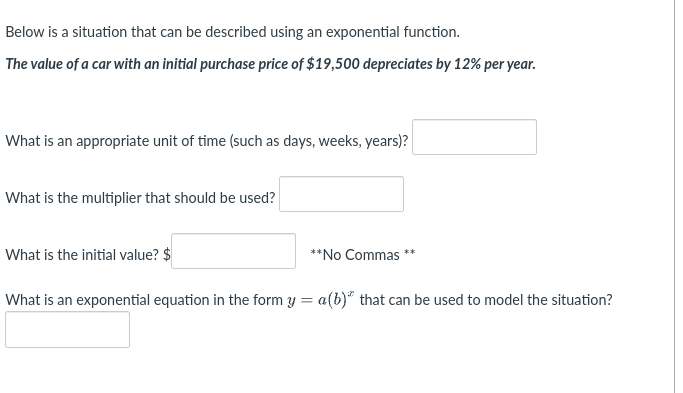
Below is a situation that can be described using an exponential function. The value of a car with an initial purchase price of $19,500 depreciates by 12% per year. What is an appro... Below is a situation that can be described using an exponential function. The value of a car with an initial purchase price of $19,500 depreciates by 12% per year. What is an appropriate unit of time (such as days, weeks, years)? What is the multiplier that should be used? What is the initial value? What is an exponential equation in the form y = a(b)^t that can be used to model the situation?
Understand the Problem
The question presents a scenario involving the depreciation of a car's value and asks for various specifics regarding the situation, such as appropriate time units, the multiplier for depreciation, the initial value, and an exponential equation to model this depreciation.
Answer
- Appropriate unit of time: years - Multiplier: 0.88 - Initial value: 19500 - Exponential equation: \( y = 19500(0.88)^t \)
Answer for screen readers
- Appropriate unit of time: years
- Multiplier: 0.88
- Initial value: 19500
- Exponential equation: ( y = 19500(0.88)^t )
Steps to Solve
- Determine the unit of time
The appropriate unit of time for the depreciation of a car's value is years. This is because the problem states that the car depreciates by 12% per year.
- Calculate the multiplier for depreciation
To find the multiplier, subtract the depreciation rate from 1:
$$ \text{Multiplier} = 1 - \text{depreciation rate} = 1 - 0.12 = 0.88 $$
- Identify the initial value
The initial value of the car is its purchase price, which is given as $19,500. So, the initial value is:
$$ \text{Initial Value} = 19500 $$
- Formulate the exponential equation
The exponential equation that models the situation can be expressed in the form ( y = a(b)^t ):
- ( a ) represents the initial value (purchase price).
- ( b ) represents the multiplier calculated.
- ( t ) represents the time in years.
Therefore, the equation is:
$$ y = 19500(0.88)^t $$
- Appropriate unit of time: years
- Multiplier: 0.88
- Initial value: 19500
- Exponential equation: ( y = 19500(0.88)^t )
More Information
The car’s value decreases each year, and this exponential decay can be modeled using the formula provided. The multiplier reflects the remaining value of the car after each year due to depreciation.
Tips
- Confusing the depreciation rate with the multiplier; remember that the multiplier is ( 1 - \text{depreciation rate} ).
- Using incorrect time units; ensure that the unit corresponds to the depreciation rate given (in this case, years).
AI-generated content may contain errors. Please verify critical information