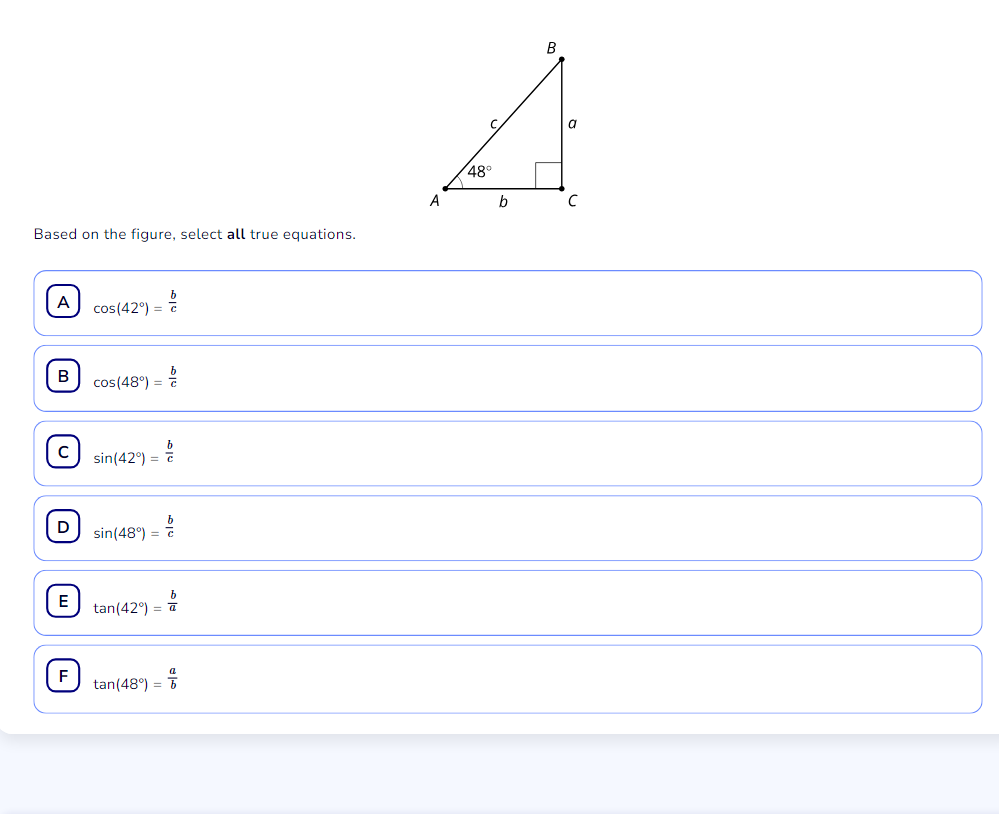
Based on the figure, select all true equations.

Steps to Solve

1. Identify Triangle Properties
   In triangle ABC, the given angles are $42^\circ$ and $48^\circ$. The third angle can be found using the property that the sum of angles in a triangle is $180^\circ$:
   $$ A + B + C = 180^\circ $$ Thus,
   $$ C = 180^\circ - 42^\circ - 48^\circ = 90^\circ $$

2. Establish Trigonometric Ratios
   For angle $A = 42^\circ$ and angle $B = 48^\circ$, we can define the trigonometric ratios:

• For angle $A$:
  $$ \cos(42^\circ) = \frac{b}{c} $$ $$ \sin(42^\circ) = \frac{a}{c} $$ $$ \tan(42^\circ) = \frac{a}{b} $$

• For angle $B$:
  $$ \cos(48^\circ) = \frac{a}{c} $$ $$ \sin(48^\circ) = \frac{b}{c} $$ $$ \tan(48^\circ) = \frac{b}{a} $$

3. Evaluate the Given Options
   Now let's check the statements one by one:

• A: $ \cos(42^\circ) = \frac{b}{c} $ (True)
• B: $ \cos(48^\circ) = \frac{b}{c} $ (False, should be $ \cos(48^\circ) = \frac{a}{c} $)
• C: $ \sin(42^\circ) = \frac{b}{c} $ (False, should be $ \sin(42^\circ) = \frac{a}{c} $)
• D: $ \sin(48^\circ) = \frac{b}{c} $ (True)
• E: $ \tan(42^\circ) = \frac{b}{a} $ (False, should be $ \tan(42^\circ) = \frac{a}{b} $)
• F: $ \tan(48^\circ) = \frac{a}{b} $ (True)

4. List the True Statements
   From the evaluations, the true equations are:

• A: $ \cos(42^\circ) = \frac{b}{c} $
• D: $ \sin(48^\circ) = \frac{b}{c} $
• F: $ \tan(48^\circ) = \frac{a}{b} $