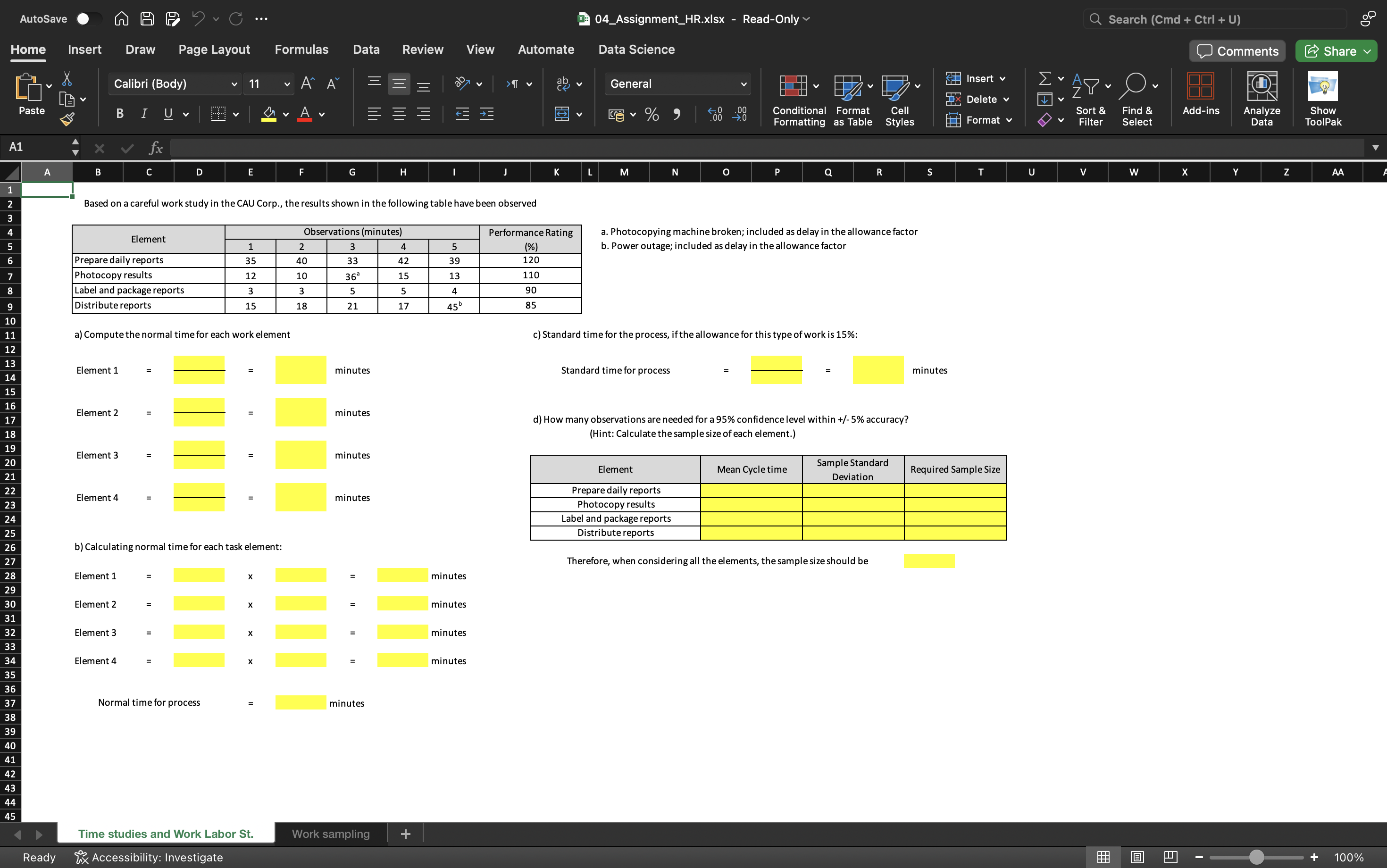
Based on a careful work study in the CAU Corp., the results shown in the following table have been observed. Compute the normal time for each work element, the standard time for th... Based on a careful work study in the CAU Corp., the results shown in the following table have been observed. Compute the normal time for each work element, the standard time for the process with a 15% allowance, and determine how many observations are needed for a 95% confidence level within +/- 5% accuracy. The task involves calculations for various work elements using provided data. Read more

Steps to Solve

1. Compute the Normal Time for Each Work Element

To find the normal time for each work element, we will calculate the average time based on observations and then adjust it using the performance rating.

• For each element, formulate the normal time as:

$$ \text{Normal Time} = \frac{\text{Sum of Observations}}{\text{Number of Observations}} \times \frac{100}{\text{Performance Rating}} $$

2. Calculating Normal Time for Each Task Element

Using the table given:

• Element 1:
  • Observations: 35, 40, 33, 42, 39
  • Performance Rating: 120%

$$ \text{Normal Time}_1 = \frac{35 + 40 + 33 + 42 + 39}{5} \times \frac{100}{120} = \frac{189}{5} \times \frac{100}{120} = 31.5 \text{ minutes} $$

• Element 2:
  • Observations: 12, 10, 36, 15, 13
  • Performance Rating: 110%

$$ \text{Normal Time}_2 = \frac{12 + 10 + 36 + 15 + 13}{5} \times \frac{100}{110} = \frac{86}{5} \times \frac{100}{110} \approx 15.64 \text{ minutes} $$

• Element 3:
  • Observations: 3, 5, 5, 4
  • Performance Rating: 90%

$$ \text{Normal Time}_3 = \frac{3 + 5 + 5 + 4}{4} \times \frac{100}{90} = \frac{17}{4} \times \frac{100}{90} \approx 18.89 \text{ minutes} $$

• Element 4:
  • Observations: 15, 18, 21, 17, 45
  • Performance Rating: 85%

$$ \text{Normal Time}_4 = \frac{15 + 18 + 21 + 17 + 45}{5} \times \frac{100}{85} = \frac{116}{5} \times \frac{100}{85} \approx 27.24 \text{ minutes} $$

3. Calculate the Standard Time for the Process

To calculate the standard time, include the 15% allowance. This is done by:

$$ \text{Standard Time} = \text{Normal Time} \times (1 + \text{Allowance}) $$

Combine the normal times:

$$ \text{Total Normal Time} = \text{Normal Time}_1 + \text{Normal Time}_2 + \text{Normal Time}_3 + \text{Normal Time}_4 $$

Then, calculate:

$$ \text{Standard Time} = \text{Total Normal Time} \times 1.15 $$

4. Determine the Required Sample Size for 95% Confidence Level

Using the formula for sample size needed for a specific confidence level:

$$ n = \left( \frac{Z \times \sigma}{E} \right)^2 $$

Where:

• $Z$ is the Z-value (1.96 for 95% confidence)
• $\sigma$ is the sample standard deviation (calculate from the observations)
• $E$ is the margin of error (5% of the total mean cycle time).

Calculate the standard deviation for each element and then compute the required sample size accordingly.