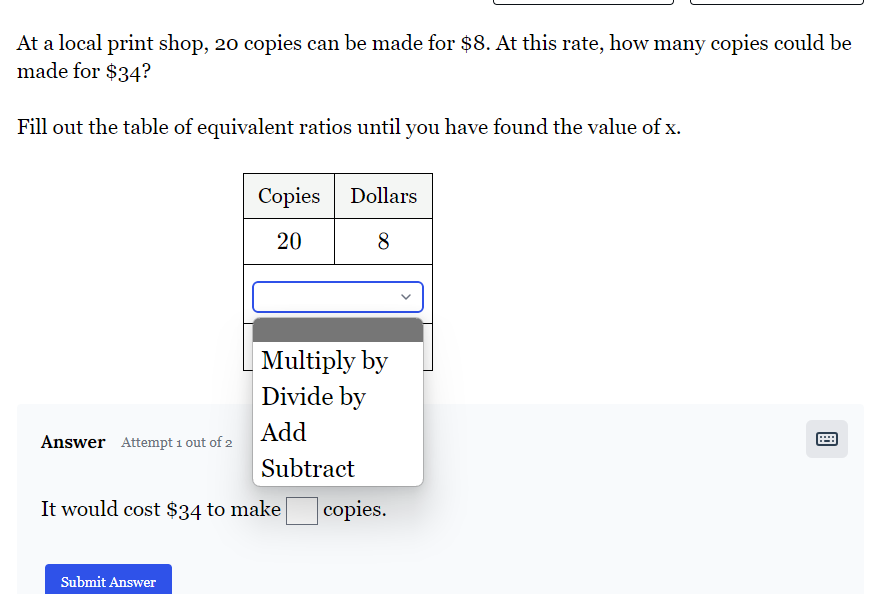
At a local print shop, 20 copies can be made for $8. At this rate, how many copies could be made for $34?
Understand the Problem
The question is asking how many copies can be made for $34 based on the rate provided (20 copies for $8). We need to determine the equivalent ratio between copies and dollars until we find the unknown value (x).
Answer
The number of copies that can be made for $34 is \( 85 \).
Answer for screen readers
It would cost $34 to make ( 85 ) copies.
Steps to Solve
- Identify the rate of copies per dollar
From the problem, we know that 20 copies cost $8.
To find the cost per copy, divide the total cost by the number of copies: $$ \text{Cost per copy} = \frac{8 \text{ dollars}}{20 \text{ copies}} = 0.4 \text{ dollars per copy} $$
- Calculate how many copies can be made for $34
Now that we know the cost per copy, we can find out how many copies can be made for $34.
By using the formula for the total number of copies based on the total dollars: $$ \text{Copies} = \frac{\text{Total dollars}}{\text{Cost per copy}} = \frac{34 \text{ dollars}}{0.4 \text{ dollars per copy}} $$
- Perform the calculation
Calculating the above expression gives: $$ \text{Copies} = 34 \div 0.4 = 85 $$
Thus, 85 copies can be made for $34.
It would cost $34 to make ( 85 ) copies.
More Information
The calculation shows that the printing rate allows for multiple copies to be made at a relatively low cost per copy. This cost-effective development is beneficial for large printing needs.
Tips
- Miscalculate the cost per copy: Ensure to divide the total cost by the correct number of copies to find the right price per unit.
- Incorrect unit usage: Always ensure the units (dollars and copies) are managed appropriately during calculations.
AI-generated content may contain errors. Please verify critical information