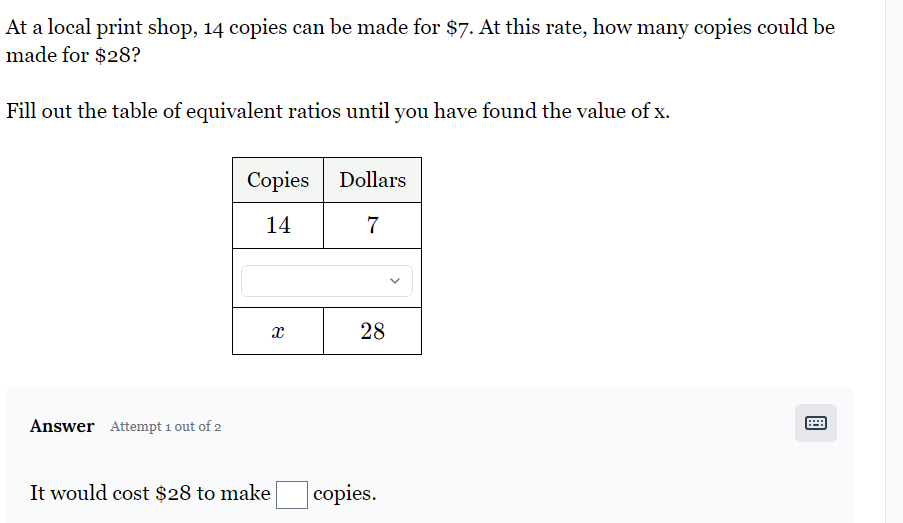
At a local print shop, 14 copies can be made for $7. At this rate, how many copies could be made for $28?
Understand the Problem
The question is asking how many copies can be made at a local print shop when $28 is spent, based on the rate of 14 copies for $7. It involves setting up a proportion to find the number of copies (x) relative to the cost.
Answer
It would cost $28 to make $56$ copies.
Answer for screen readers
It would cost $28 to make 56 copies.
Steps to Solve
- Set Up the Proportion
Start by representing the information given. You know that 14 copies cost $7. You want to find out how many copies, $x$, can be made for $28. Set up the proportion as follows:
$$ \frac{14 \text{ copies}}{7 \text{ dollars}} = \frac{x \text{ copies}}{28 \text{ dollars}} $$
- Cross Multiply
To solve for $x$, cross multiply the terms of the proportion:
$$ 14 \times 28 = 7 \times x $$
This gives:
$$ 392 = 7x $$
- Solve for x
Next, isolate $x$ by dividing both sides of the equation by 7:
$$ x = \frac{392}{7} $$
- Calculate the Result
Perform the division:
$$ x = 56 $$
So, the number of copies that can be made is 56.
It would cost $28 to make 56 copies.
More Information
At the local print shop, the cost per copy can be inferred from the given ratio. For every $7 spent, 14 copies can be made. This leads to a unit price of $0.50 per copy, confirming that $28 will buy 56 copies.
Tips
- Not correctly setting up the proportion: Ensure the ratios are aligned correctly according to copies and cost.
- Miscalculating the cross multiplication: Double-check arithmetic when performing multiplication.
- Forgetting to divide when solving for $x$: Always isolate the variable correctly.
AI-generated content may contain errors. Please verify critical information