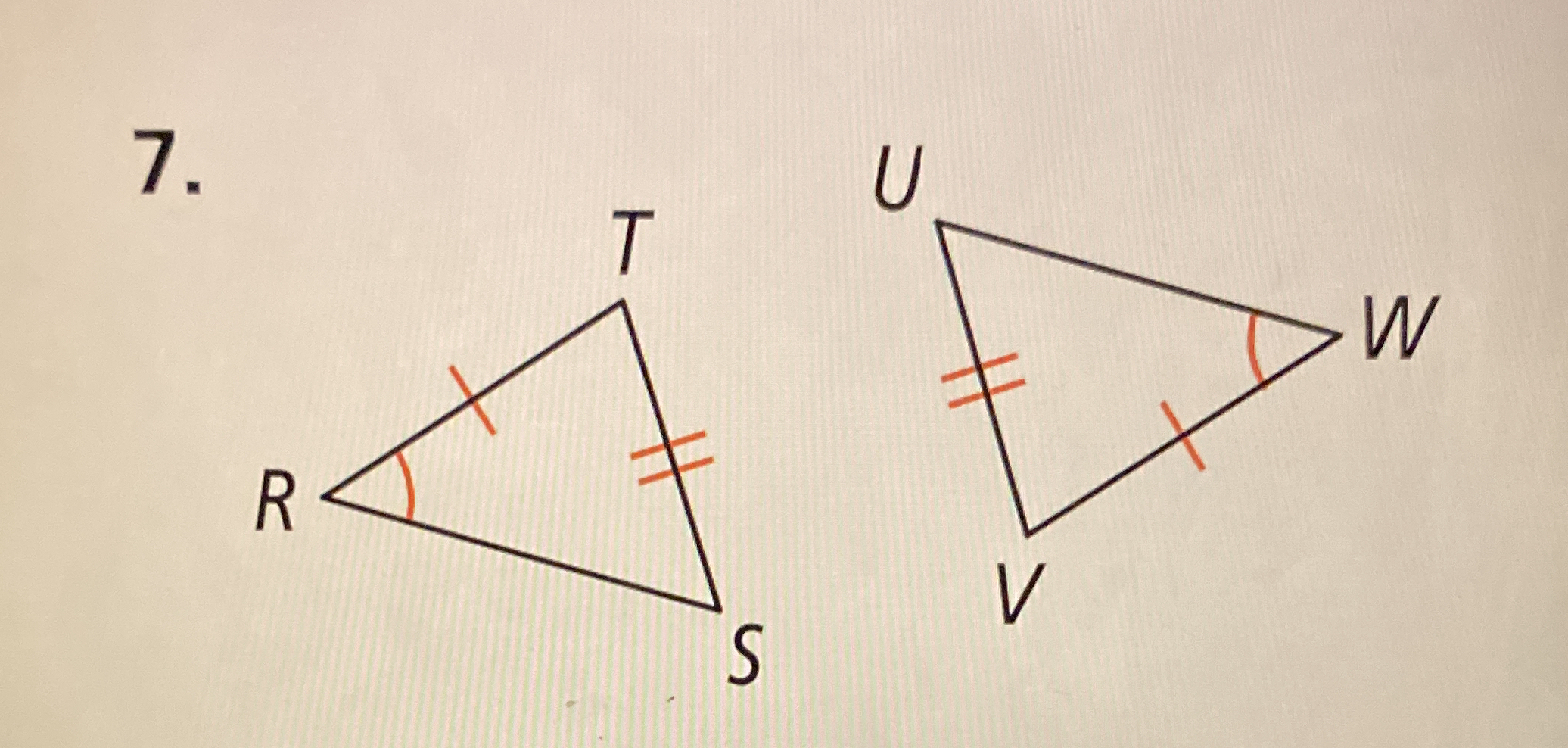
Analyze the properties of the two triangles shown in the image.
Understand the Problem
The question presents two triangles with marked equal angles and asks to analyze their properties, likely in the context of congruence or similarity.
Answer
The triangles \( RST \) and \( UVW \) are similar.
Answer for screen readers
The triangles ( RST ) and ( UVW ) are similar.
Steps to Solve
-
Identify Given Information
The triangles ( RST ) and ( UVW ) have marked equal angles. Specifically, angles ( R ) and ( U ) are equal, as indicated by the arcs, and angles ( S ) and ( V ) are also equal. -
Determine Unknown Angles
Since the sum of the angles in any triangle is ( 180^\circ ), we can express the unknown angles in terms of the known angles:- For triangle ( RST ): $$ \angle T = 180^\circ - (\angle R + \angle S) $$
- For triangle ( UVW ): $$ \angle W = 180^\circ - (\angle U + \angle V) $$
-
Compare Angles to Establish Similarity
Since we know ( \angle R = \angle U ) and ( \angle S = \angle V ), we can substitute those into the equations:- Both triangles have their angles expressed as: $$ \angle T = 180^\circ - (\angle U + \angle V) = \angle W $$
-
Conclusion of Similarity
Since both triangles have corresponding angles that are equal, we conclude that triangles ( RST ) and ( UVW ) are similar by the Angle-Angle (AA) postulate.
The triangles ( RST ) and ( UVW ) are similar.
More Information
Triangles are similar when they have equal corresponding angles. This property is fundamental in geometry, particularly regarding the study of triangle congruence and similarity.
Tips
- Mistaking equal angles for congruence of triangles. Similar triangles do not have to be the same size.
- Forgetting to account for all angles when concluding similarity; each corresponding angle must be checked.
AI-generated content may contain errors. Please verify critical information