Analyze the mechanical stresses on the rectangular object given the pressures and material strengths.
Understand the Problem
The question is asking about a mechanical problem involving stress and material properties, specifically pertaining to a rectangular object subjected to different pressures. It requires the application of material strength concepts, likely to determine safety or failure under the given loads following the provided material specifications.
Answer
The total stress is $80 \, \text{MPa}$; the component is safe since $80 \, \text{MPa} < 400 \, \text{MPa}$.
Answer for screen readers
The total stress acting on the object is $80 , \text{MPa}$, which is below the yield strength of $400 , \text{MPa}$. Thus, the mechanical component is safe under the given conditions.
Steps to Solve
-
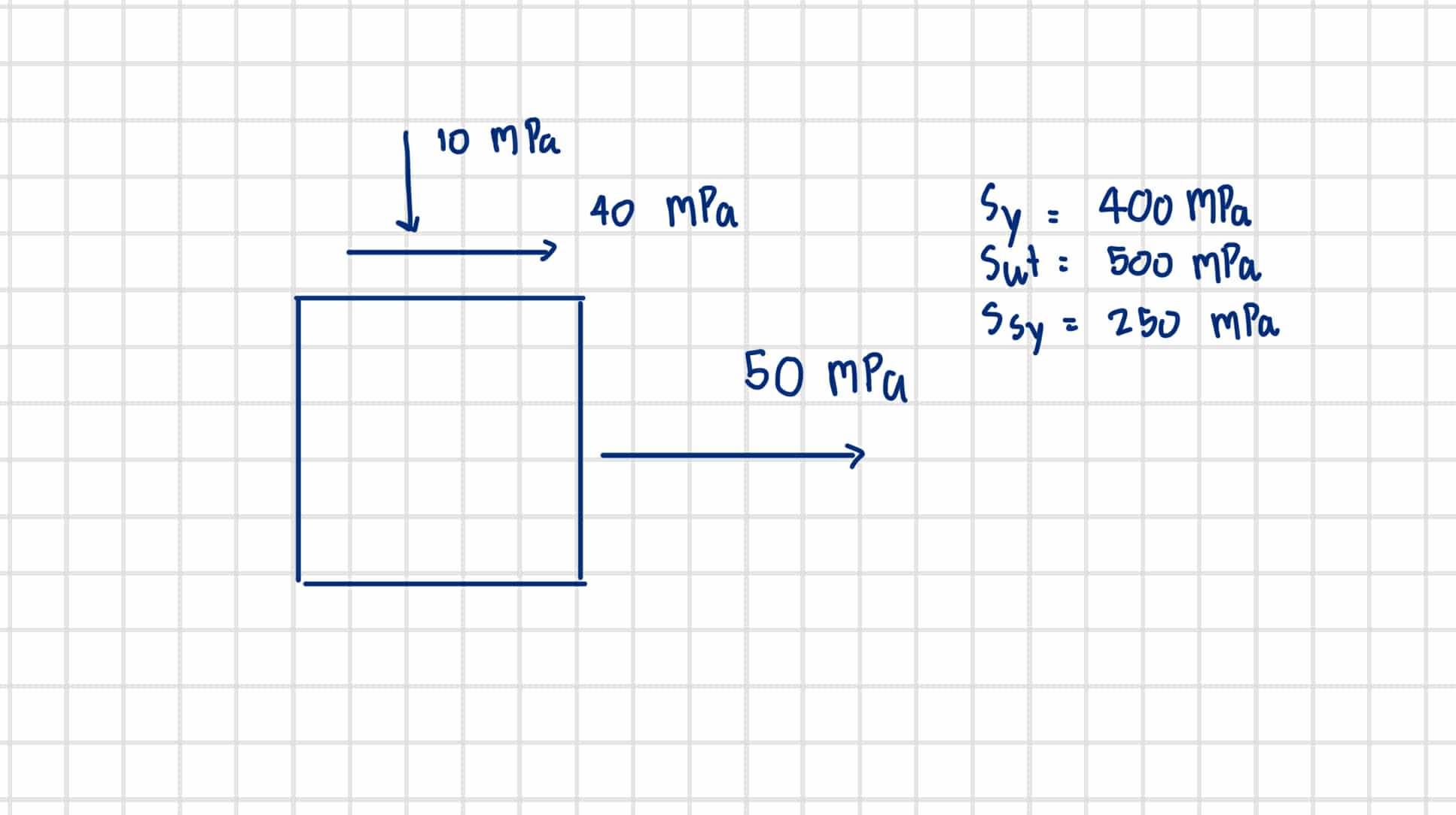
Identify Stresses Acting on the Object
The object is subjected to different pressures. We have:- A vertical load creating a stress of $10 , \text{MPa}$ (compression).
- A horizontal load creating a stress of $40 , \text{MPa}$ (tension).
- An additional horizontal stress of $50 , \text{MPa}$.
-
Calculate the Total Stress on the Object
Combine the stresses to find the maximum stress in the object. The total stress ($\sigma_{total}$) is given by:
$$ \sigma_{total} = \sigma_{tension} - \sigma_{compression} $$
Substituting values:
$$ \sigma_{total} = 40 , \text{MPa} + 50 , \text{MPa} - 10 , \text{MPa} = 80 , \text{MPa} $$ -
Compare Total Stress with Material Strength
The material properties provided are:- Yield Strength ($S_y$) = $400 , \text{MPa}$
- Ultimate Tensile Strength ($S_{ut}$) = $500 , \text{MPa}$
- Shear Yield Strength ($S_{sy}$) = $250 , \text{MPa}$
Compare $\sigma_{total}$ with $S_y$ to evaluate safety:
Since $80 , \text{MPa} < 400 , \text{MPa}$, the material is safe under these conditions.
-
Conclusion: Safety Assessment
The object can safely withstand the applied loads without failure since the total stress is below the yield strength.
The total stress acting on the object is $80 , \text{MPa}$, which is below the yield strength of $400 , \text{MPa}$. Thus, the mechanical component is safe under the given conditions.
More Information
Stress calculations are crucial in material science to ensure structures and components can withstand operating conditions without failing.
Tips
- Incorrectly summing stresses: Ensure to clearly distinguish between tensile and compressive stresses when combining them.
- Ignoring material properties: Always refer to the correct yield or ultimate strength to assess safety.
AI-generated content may contain errors. Please verify critical information