आलगढ़ीय विधि से हल करें: x - y = 1, 2x + 3y = 12।
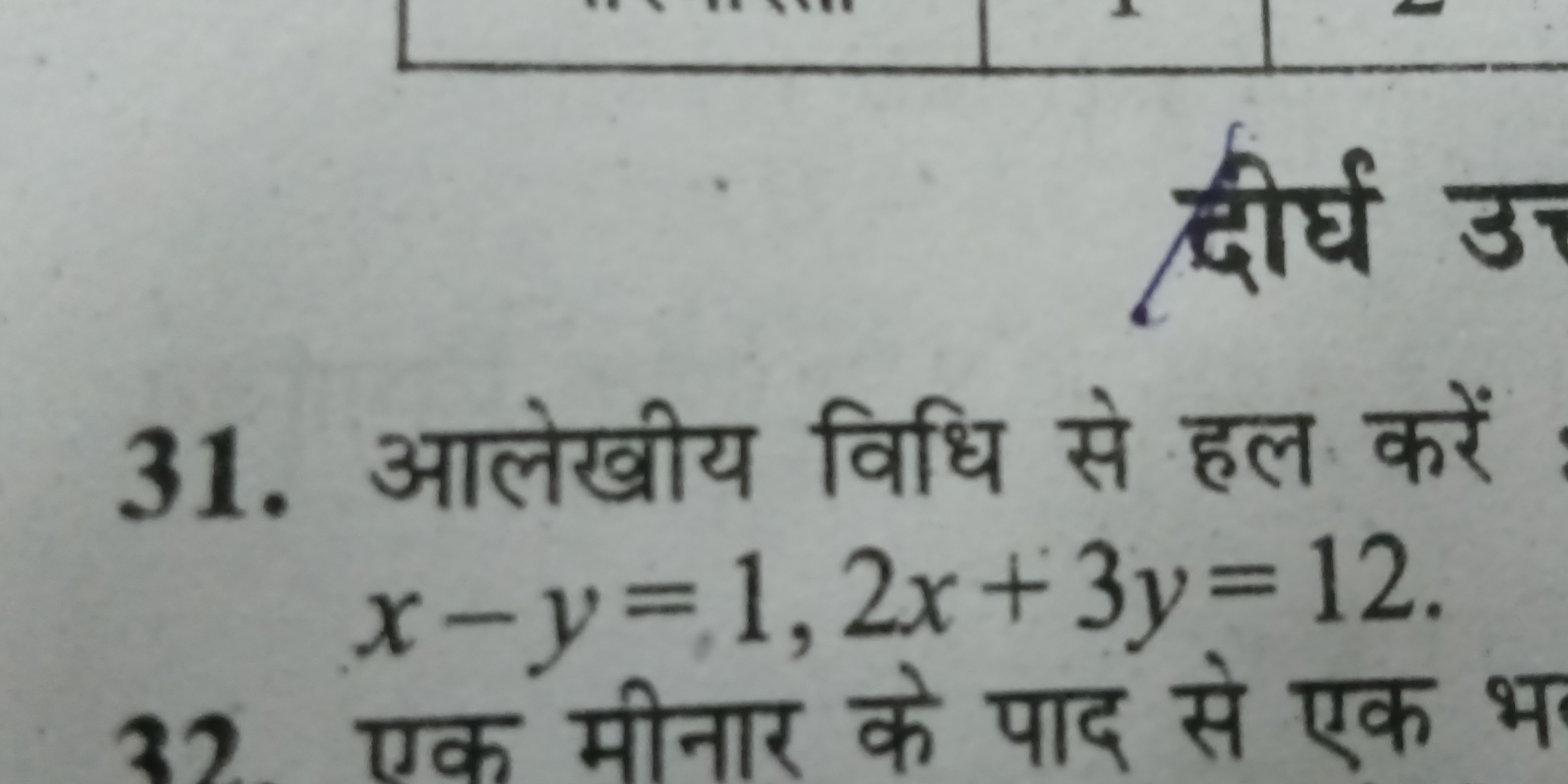
Understand the Problem
यह प्रश्न सामंजस्य विधि से दो समीकरणों को हल करने का निर्देश देता है। दिए गए समीकरण हैं: x - y = 1 और 2x + 3y = 12। हमें इन समीकरणों का समाधान ढूंढना है।
Answer
$x = 3$, $y = 2$
Answer for screen readers
$x = 3$, $y = 2$
Steps to Solve
- समीकरण को पुनः व्यवस्थित करें
पहले समीकरण $x - y = 1$ को $x$ के लिए हल करें:
$$ x = y + 1 $$
- पहले समीकरण का मान दूसरे समीकरण में डालें
अब $x$ के मान को दूसरे समीकरण $2x + 3y = 12$ में डालें:
$$ 2(y + 1) + 3y = 12 $$
- समीकरण को सरल करें
समीकरण को सरल करते हैं:
$$ 2y + 2 + 3y = 12 $$
- $y$ के लिए समीकरण हल करें
अब $y$ के लिए हल करें:
$$ 5y + 2 = 12 $$
इससे हमें मिलेगा:
$$ 5y = 12 - 2 $$
$$ 5y = 10 $$
$$ y = 2 $$
- $y$ के मान का उपयोग करके $x$ का मान पाएँ
अब, $y$ का मान $2$ है। इसे पहले समीकरण में डालें:
$$ x = y + 1 $$
$$ x = 2 + 1 $$
$$ x = 3 $$
$x = 3$, $y = 2$
More Information
यह उत्तर दो रेखीय समीकरणों को हल करने के लिए सामंजस्य विधि का उपयोग करके प्राप्त हुआ है। समीकरणों का हल खोजने के लिए, हमने पहले एक समीकरण से एक चर का मान निकाला और फिर उसे दूसरे समीकरण में प्रतिस्थापित किया।
Tips
- समीकरण को गलत स्थान पर प्रतिस्थापित करना, जो गलत उत्तर दे सकता है।
- समीकरण को सरल करते समय जोड़-घटाव में गलती करना।
AI-generated content may contain errors. Please verify critical information