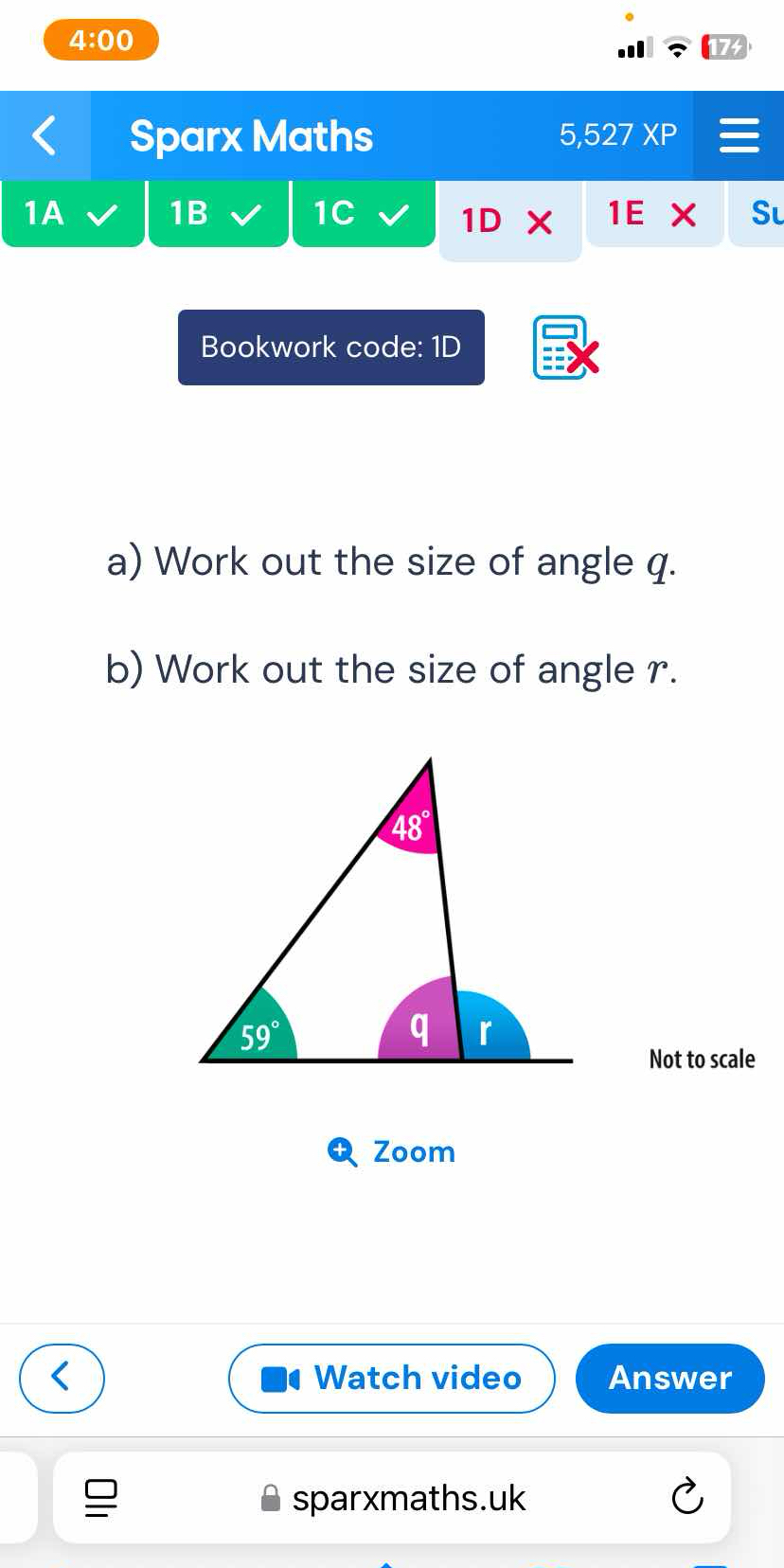
a) Work out the size of angle q. b) Work out the size of angle r.
Understand the Problem
The question is asking to calculate the sizes of angles q and r in a triangle, given the angles of 48° and 59°.
Answer
Angle $q = 73^\circ$, angle $r = 132^\circ$.
Answer for screen readers
The sizes of the angles are:
Angle $q = 73^\circ$
Angle $r = 132^\circ$
Steps to Solve
-
Understand the Triangle Sum Theorem
In any triangle, the sum of all interior angles is always $180^\circ$. This means we can find the missing angles by summing the known angles and subtracting from $180^\circ$. -
Calculate Angle $q$
First, we know two angles: $48^\circ$ and $59^\circ$. We can add these two angles together:
$$ 48^\circ + 59^\circ = 107^\circ $$
Now, we can find angle $q$ by subtracting this from $180^\circ$:
$$ q = 180^\circ - 107^\circ $$
This gives us:
$$ q = 73^\circ $$ -
Calculate Angle $r$
Now, to find angle $r$, we use the relationship within the triangle again. Since angle $r$ is adjacent to angle $q$, we know:
$$ r = 180^\circ - 48^\circ $$
This results in:
$$ r = 132^\circ $$
The sizes of the angles are:
Angle $q = 73^\circ$
Angle $r = 132^\circ$
More Information
In a triangle, the sum of the angles always equals $180^\circ$. This property is fundamental for solving problems related to angles in triangles.
Tips
- Forgetting that the sum of angles in a triangle is $180^\circ$.
- Miscalculating the addition when summing known angles.
- Confusing the relationships between angles (e.g., assuming all angles can be calculated directly without considering their position).
AI-generated content may contain errors. Please verify critical information