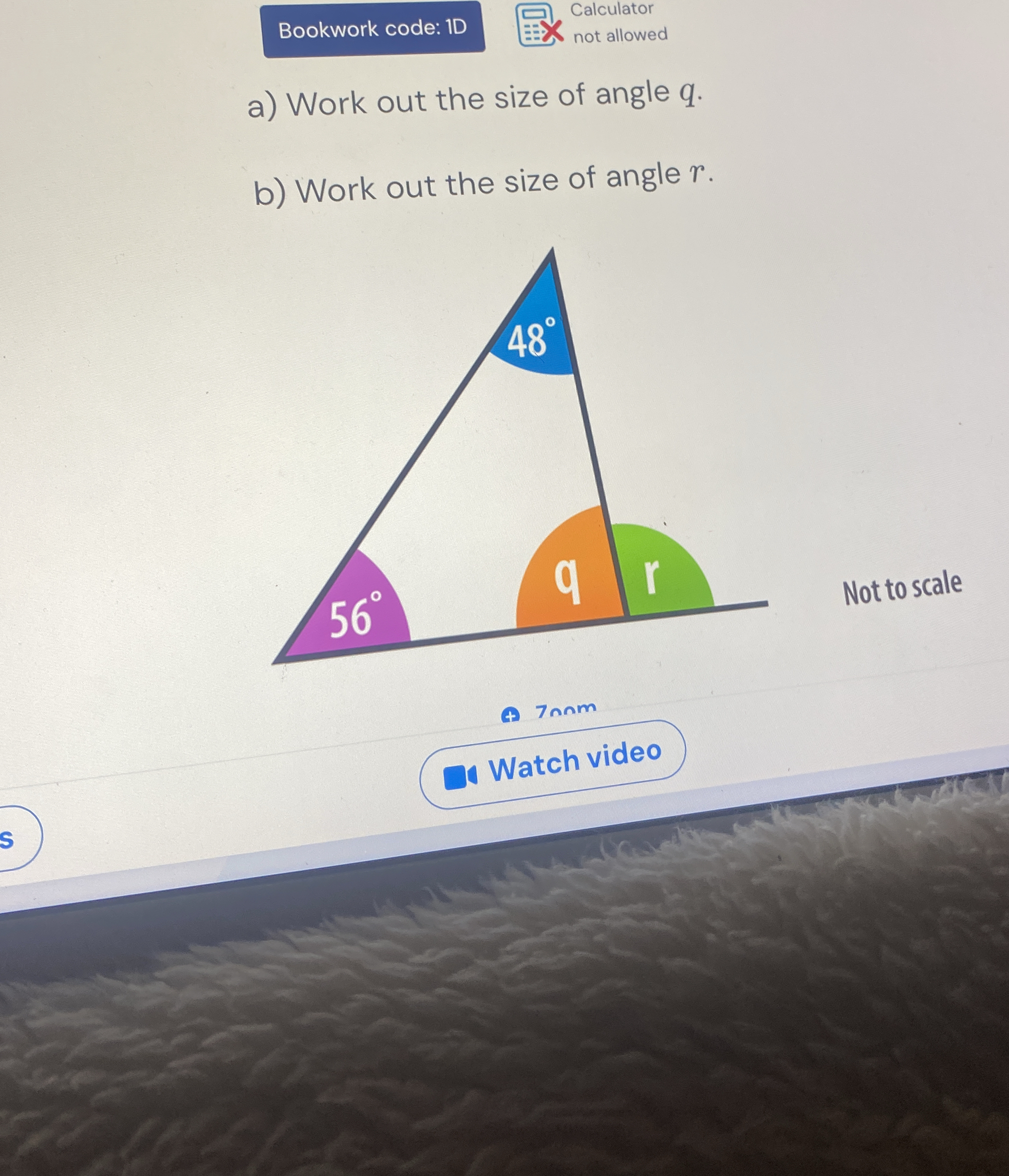
a) Work out the size of angle q. b) Work out the size of angle r.
Understand the Problem
The question is asking to calculate the sizes of two angles, q and r, in a triangle, given the sizes of two other angles. To solve this, we need to use the fact that the sum of all angles in a triangle is 180 degrees.
Answer
The measures of angles are connected as $q + r = 76^\circ$. Specific values can't be determined without further information.
Answer for screen readers
The size of angle $q$ is $76^\circ - r$.
The size of angle $r$ can take multiple valid values depending on the choice of $q$ within the constraints. However, you need to know either $q$ or $r$ specifically to find the exact measures.
Steps to Solve
-
Identify the sum of angles in a triangle
In any triangle, the sum of all interior angles is always $180^\circ$. Therefore, we can set up the equation:
$$ q + r + 48^\circ + 56^\circ = 180^\circ $$ -
Calculate the known angles' sum
First, let's calculate the sum of the known angles:
$$ 48^\circ + 56^\circ = 104^\circ $$ -
Set up the equation for angles q and r
Now substitute the sum of the known angles back into the equation:
$$ q + r + 104^\circ = 180^\circ $$ -
Solve for q + r
Isolate the variables $q$ and $r$ by subtracting $104^\circ$ from both sides:
$$ q + r = 180^\circ - 104^\circ $$
$$ q + r = 76^\circ $$ -
Use one angle to find the other
For angle $q$, we can express it in terms of angle $r$:
$$ q = 76^\circ - r $$ -
Recall that angle r is left over
Since we know that $r$ is one of the remaining angles to find, choose it as a portion to express in terms of $q$.
The size of angle $q$ is $76^\circ - r$.
The size of angle $r$ can take multiple valid values depending on the choice of $q$ within the constraints. However, you need to know either $q$ or $r$ specifically to find the exact measures.
More Information
The sum of the angles in a triangle is a foundational concept in geometry. This problem illustrates how to find remaining angles when some are known. Angles can vary as long as they adhere to the property of summing to 180 degrees.
Tips
- Failing to remember that all angles in a triangle must sum to 180 degrees.
- Forgetting to subtract the sum of the known angles from 180 degrees.
AI-generated content may contain errors. Please verify critical information