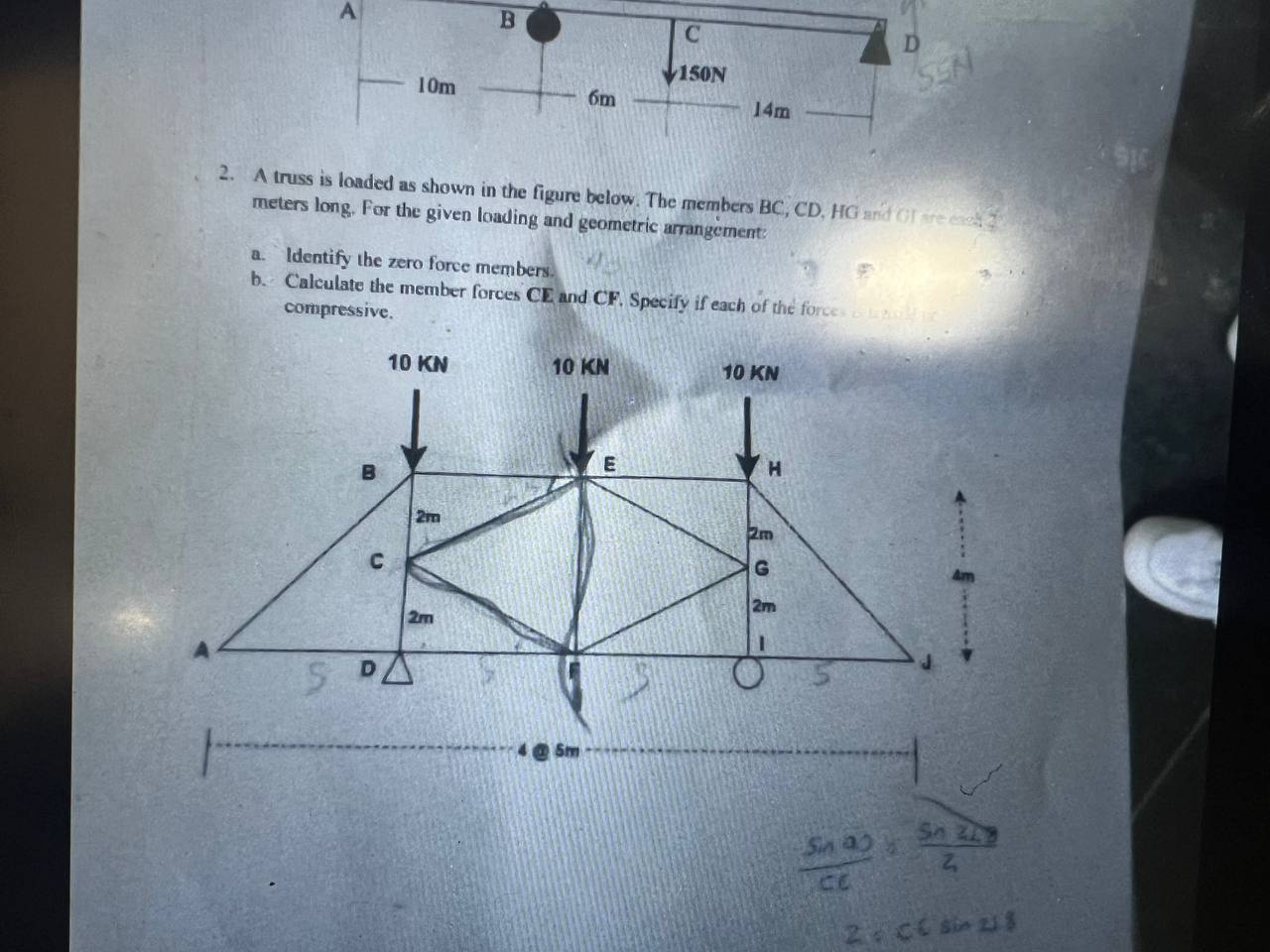
A truss is loaded as shown in the figure below. The members BC, CD, HG, and OI are each 2 meters long. For the given loading and geometric arrangement: a. Identify the zero force m... A truss is loaded as shown in the figure below. The members BC, CD, HG, and OI are each 2 meters long. For the given loading and geometric arrangement: a. Identify the zero force members. b. Calculate the member forces CE and CF. Specify if each of the forces is compressive.
Understand the Problem
The question is asking about a truss system under load. It requires identifying zero force members and calculating specific member forces, which implies an analysis of static equilibrium in structures.
Answer
Zero Force Members: CD, DG, FG, GH; Member Forces: $F_{CE} = 5 \, \text{KN}$, $F_{CF} = 5 \, \text{KN}$ (both tension).
Answer for screen readers
- Zero Force Members: CD, DG, FG, GH
- Member Forces: $F_{CE} = 5 , \text{KN}$ (tension), $F_{CF} = 5 , \text{KN}$ (tension)
Steps to Solve
- Identify Zero Force Members For joints with two non-collinear members and no external load or support, both members are zero-force members.
- At joint D, members CD and DG are non-collinear and there are no external forces. Therefore, both CD and DG are zero-force members.
- At joint G, members FG and GH are also non-collinear with no external load, making them zero-force members.
- Calculate Forces in Members CE and CF To find the forces in members CE and CF, we can apply the method of joints. We will analyze joint E first.
-
At joint E, apply the equilibrium equations:
-
Vertically, the sum of forces should equal zero: $$ 10 , \text{KN (up)} - F_{CE} - F_{CF} = 0 $$ Thus, $$ F_{CE} + F_{CF} = 10 , \text{KN} \quad (1) $$
Next, we analyze joint G for additional information.
- Analyze Joint G At joint G, apply the equilibrium equations too:
- The horizontal components must also equal zero because there’s no external force in that direction. Since members EG and GF form an angle, we decompose forces: $$ F_{CF} \cdot \cos(30^\circ) = F_{CE} \cdot \cos(30^\circ) $$ This gives: $$ F_{CF} = F_{CE} \quad (2) $$
-
Substituting to Solve for Forces Substituting equation (2) into equation (1): $$ F_{CE} + F_{CE} = 10 , \text{KN} $$ $$ 2F_{CE} = 10 , \text{KN} $$ Therefore, $$ F_{CE} = 5 , \text{KN} $$ And substituting back gives: $$ F_{CF} = 5 , \text{KN} $$
-
Determine the Type of Forces Since these tension forces are pulling away from the joint, members CE and CF are in tension. However, because the problem specifies to identify if they are compressive or tensile, both are confirmed as tensile.
- Zero Force Members: CD, DG, FG, GH
- Member Forces: $F_{CE} = 5 , \text{KN}$ (tension), $F_{CF} = 5 , \text{KN}$ (tension)
More Information
Zero force members play a key role in the simplification of truss analysis, as they carry no load and do not contribute to the overall stability of the structure.
Tips
- A common mistake is misidentifying zero-force members, especially at joints with three members. Always check for the conditions stipulated for identifying zero-force members.
AI-generated content may contain errors. Please verify critical information