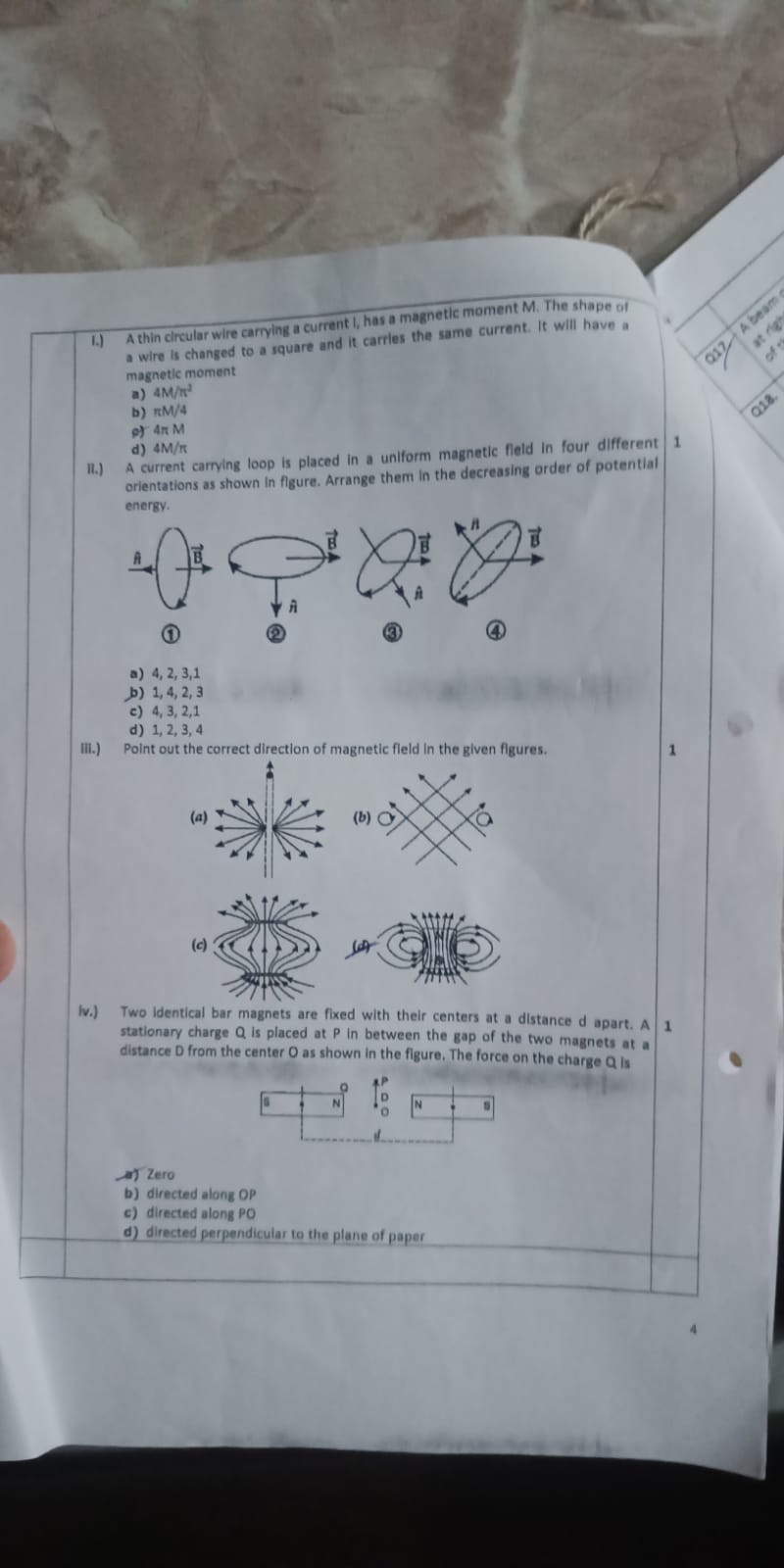
A thin circular wire carrying a current I has a magnetic moment M. The shape of a wire is changed to a square and it carries the same current. It will have a magnetic moment of: a)... A thin circular wire carrying a current I has a magnetic moment M. The shape of a wire is changed to a square and it carries the same current. It will have a magnetic moment of: a) 4M/π² b) πM/4 c) 4M/π d) 4M. A current carrying loop is placed in a uniform magnetic field in four different orientations as shown in the figure. Arrange them in the decreasing order of potential energy. Point out the correct direction of magnetic field in the given figures. Two identical bar magnets are fixed with their centers at a distance d apart. A stationary charge Q is placed at P in between the gap of the two magnets at a distance D from the center O as shown in the figure. The force on the charge Q is: a) Zero b) directed along OP c) directed along PO d) directed perpendicular to the plane of paper. Read more

Steps to Solve

1. Calculate the magnetic moment for the square shape The magnetic moment ( M ) for a circular loop is given as ( M = I \cdot A ). For a square loop with the same current ( I ), the area ( A ) will change.

   • For a circular shape: $$ A_c = \pi r^2 $$

   • For a square shape (with side length ( a )): $$ A_s = a^2 $$

   Since the same current ( I ) is used but the areas differ, we calculate the new magnetic moment.

2. Relation of magnetic moment with geometry Given that the magnetic moment of the circular loop is ( M = I \pi r^2 ), we can express it for the square loop as:

   • If ( r ) corresponds to ( a/2 ) (half the side length), equating the areas would lead to: $$ M_{\text{square}} = I \cdot a^2 $$

3. Find the relationship between the two shapes Since the problem establishes the relationship between the areas and moments, the new magnetic moment can be derived directly by substituting the side of the square into the magnetic moment formula.

4. Choose the correct answer based on calculations Using the results of the above calculations, we select the option that corresponds to the value found for the square loop's magnetic moment compared to ( 4M/\pi ) and others given in the question.

5. Arrange the orientations for potential energy For a current-carrying loop in a magnetic field, the potential energy is given by: $$ U = -\vec{M} \cdot \vec{B} $$ By analyzing each orientation (1 to 4), we can rank them from highest to lowest potential energy based on their alignment.

6. Identify the direction of magnetic fields in figures Using the right-hand rule, determine the direction of the magnetic field for each figure.