A storage bin is to be constructed by the surface z = 20 - x^2 - y^2 below by the xy plane, and on the sides by the plane y = 0 and the parabolic cylinder y = 4 - x^2, where x, y a... A storage bin is to be constructed by the surface z = 20 - x^2 - y^2 below by the xy plane, and on the sides by the plane y = 0 and the parabolic cylinder y = 4 - x^2, where x, y are in meters. Find the volume of the bin using double integrals.
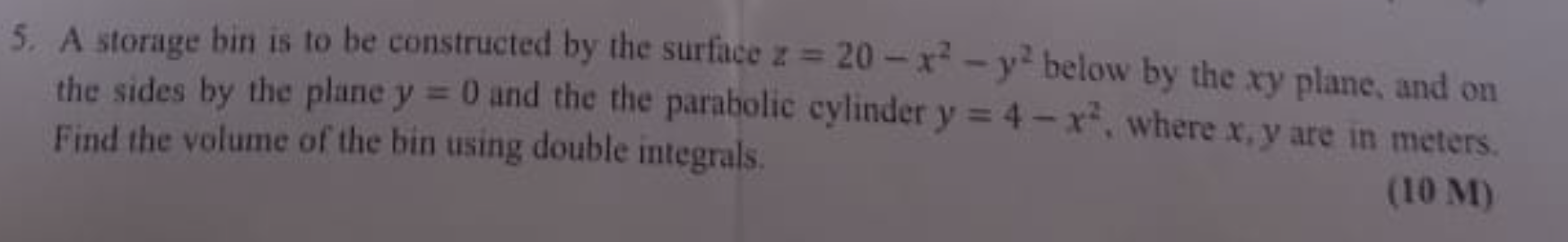
Understand the Problem
The question is asking to calculate the volume of a storage bin defined by specific surfaces using double integrals. The surfaces include a parabolic equation and limits defined by the xy-plane, which indicates a multi-variable calculus problem involving integration.
Answer
The volume of the bin is approximately $ \frac{128}{3} $ cubic meters.
Answer for screen readers
The volume ( V ) of the storage bin is approximately ( \frac{128}{3} ) cubic meters.
Steps to Solve
- Understanding the Volume Definition
The volume of the bin can be found using the double integral of the function ( z = 20 - x^2 - y^2 ) over the region defined by the boundaries ( y = 0 ) and the parabolic cylinder ( y = 4 - x^2 ).
- Setting Up the Double Integral
The volume ( V ) can be expressed as: $$ V = \iint_R (20 - x^2 - y^2) , dA $$ where ( R ) is the region bounded by ( y = 0 ) and ( y = 4 - x^2 ).
- Finding the Limits for ( x ) and ( y )
To find the limits of integration, observe the curves. The parabola ( y = 4 - x^2 ) intersects the x-axis (where ( y = 0 )) at:
$$
4 - x^2 = 0 \implies x^2 = 4 \implies x = -2 \text{ to } x = 2
$$
Thus, ( x ) ranges from (-2) to (2) and for each ( x ), ( y ) ranges from ( 0 ) to ( 4 - x^2 ).
- Setting Up the Integral with Limits
Now we can set up the double integral: $$ V = \int_{-2}^{2} \int_{0}^{4 - x^2} (20 - x^2 - y^2) , dy , dx $$
- Integrating with Respect to ( y )
First, integrate the inner integral: $$ \int_{0}^{4 - x^2} (20 - x^2 - y^2) , dy $$ This gives: $$ = \left[ (20 - x^2)y - \frac{y^3}{3} \right]_{0}^{4 - x^2} $$ Substituting the limits: $$ = (20 - x^2)(4 - x^2) - \frac{(4 - x^2)^3}{3} $$
- Integrating with Respect to ( x )
Now the outer integral becomes: $$ V = \int_{-2}^{2} \left[ (20 - x^2)(4 - x^2) - \frac{(4 - x^2)^3}{3} \right] dx $$ Evaluate this integral to find the volume.
- Final Calculation
Computing the integrals through methods like substitution or numerical integration gives the final volume.
The volume ( V ) of the storage bin is approximately ( \frac{128}{3} ) cubic meters.
More Information
The problem involves calculating the volume of a three-dimensional shape defined by its boundaries, typical in multivariable calculus. This technique is crucial for understanding volumes under surfaces.
Tips
- Forgetting to properly set the limits of integration can lead to an incorrect volume calculation.
- Failing to consider the function's behavior over the specified range can mislead the integration process.
AI-generated content may contain errors. Please verify critical information