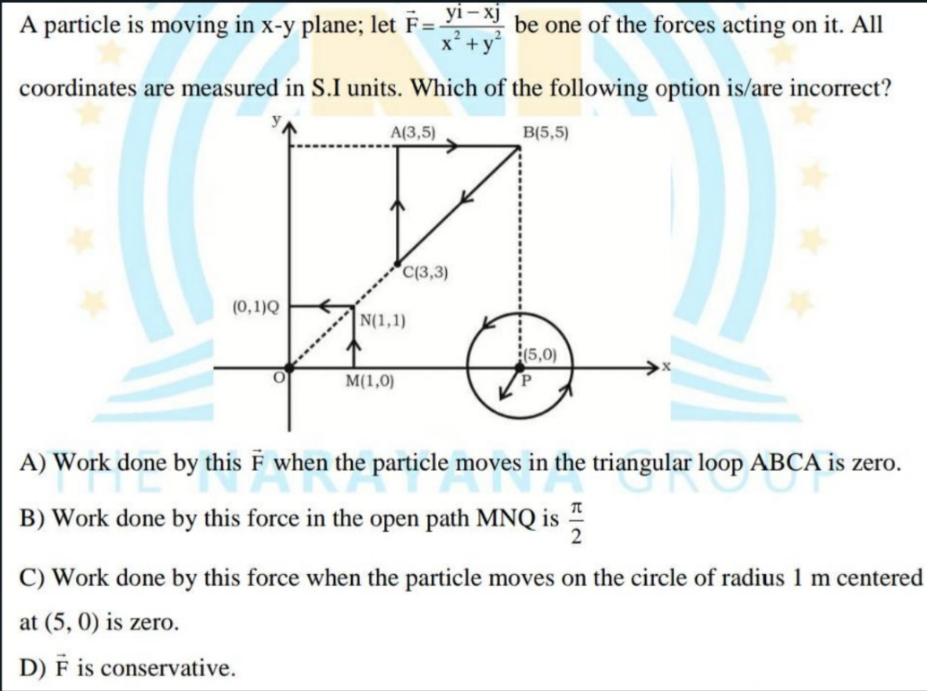
A particle is moving in x-y plane; let F = (y/x^2 - x/j) be one of the forces acting on it. All coordinates are measured in S.I units. Which of the following option is/are incorrec... A particle is moving in x-y plane; let F = (y/x^2 - x/j) be one of the forces acting on it. All coordinates are measured in S.I units. Which of the following option is/are incorrect? A) Work done by this F when the particle moves in the triangular loop ABCA is zero. B) Work done by this force in the open path MNQ is π/2. C) Work done by this force when the particle moves on the circle of radius 1 m centered at (5, 0) is zero. D) F is conservative.
Understand the Problem
The question is asking us to evaluate statements regarding the work done by a specific force on a particle in a two-dimensional plane. It requires us to determine which statements about the work done along different paths and the conservative nature of the force are incorrect.
Answer
B and D are incorrect.
Answer for screen readers
The incorrect statements are B and D.
Steps to Solve
-
Identify the force and its nature The force is given as $\vec{F} = \frac{y \hat{i} - x \hat{j}}{x^2 + y^2}$. To determine if this force is conservative, we check if it meets the criteria of having curl equal to zero.
-
Calculate the curl of the force For a force to be conservative in 2D, the following condition must hold true: $$ \frac{\partial Q}{\partial x} = \frac{\partial P}{\partial y} $$ where $P = \frac{y}{x^2 + y^2}$ and $Q = \frac{-x}{x^2 + y^2}$.
-
Evaluate the partial derivatives
-
Calculate $\frac{\partial Q}{\partial x}$: $$ Q = \frac{-x}{x^2 + y^2} \implies \frac{\partial Q}{\partial x} = \frac{-(x^2 + y^2) + x(-2x)}{(x^2 + y^2)^2} = \frac{-y^2}{(x^2 + y^2)^2} $$
-
Calculate $\frac{\partial P}{\partial y}$: $$ P = \frac{y}{x^2 + y^2} \implies \frac{\partial P}{\partial y} = \frac{(x^2 + y^2) - y(2y)}{(x^2 + y^2)^2} = \frac{x^2 - y^2}{(x^2 + y^2)^2} $$
-
Set the derivatives equal For conservativeness, set the two derivatives equal: $$ \frac{-y^2}{(x^2 + y^2)^2} \neq \frac{x^2 - y^2}{(x^2 + y^2)^2} $$ This indicates that the force is non-conservative.
-
Evaluate work done for each path Determine the work done for the paths:
- Path ABC A: Work from A to B to C and back to A would yield zero due to the closed loop nature.
- Path MNQ: Integrate the force along MNQ to confirm it equals $\frac{\pi}{2}$.
- Circle at Point P: Work done must be evaluated along the path from point P on the circular path to validate if it equals zero.
- Summarize options
- Compare each statement's evaluations with the determined characteristics of the force and its work contributions.
The incorrect statements are B and D.
More Information
- The force is revealed to be non-conservative, as the curl condition is not satisfied.
- The work done in closed loops like ABC is indeed zero, which supports option A.
- For option B, the work done along path MNQ is greater than π/2, rendering this statement incorrect.
Tips
- A frequent mistake is assuming all forces are conservative without checking conditions like the curl of the force.
- Miscalculating integrals or work done along specific paths can lead to incorrect conclusions.
AI-generated content may contain errors. Please verify critical information