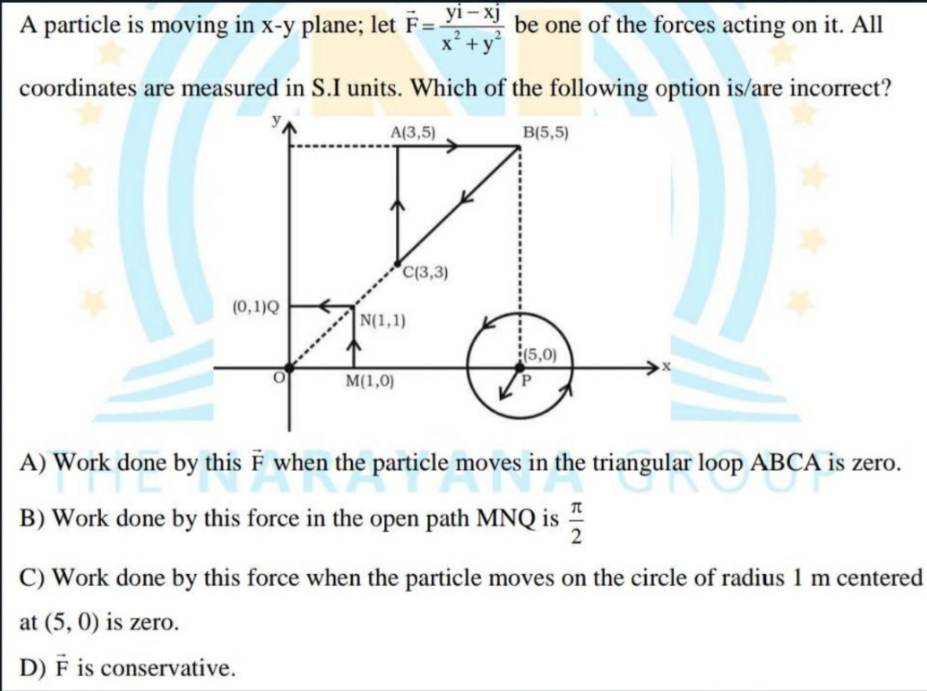
A particle is moving in x-y plane; let F = (y i - x j) / (x^2 + y^2) be one of the forces acting on it. All coordinates are measured in S.I units. Which of the following option is/... A particle is moving in x-y plane; let F = (y i - x j) / (x^2 + y^2) be one of the forces acting on it. All coordinates are measured in S.I units. Which of the following option is/are incorrect? A) Work done by this F when the particle moves in the triangular loop ABCA is zero. B) Work done by this force in the open path MNQ is π/2. C) Work done by this force when the particle moves on the circle of radius 1 m centered at (5,0) is zero. D) F is conservative.
Understand the Problem
The question is asking about the work done by a force acting on a particle moving in the x-y plane, specifically which of the provided options regarding the work done under different paths and conditions is incorrect.
Answer
B, D
Answer for screen readers
The incorrect options are B) work done in the open path MNQ is $\frac{\pi}{2}$ and D) $\mathbf{F}$ is conservative.
Steps to Solve
-
Identify the Force Field Type Determine if the force field $ \mathbf{F} = \frac{y \mathbf{i} - x \mathbf{j}}{x^2 + y^2} $ is conservative. A force is conservative if the work done in a closed path is zero.
-
Check Work Done Along Closed Path (ABCA) Evaluate if the work done around the triangular loop ABCA is zero. Using the line integral, if the path is closed, calculate: $$ W_{closed} = \oint_C \mathbf{F} \cdot d\mathbf{r} $$ If it is a closed loop and the field is conservative, the result should be zero.
-
Evaluate Work Done in Open Path (MNQ) Calculate the work done along the open path from M to N to Q. The work can be calculated using: $$ W_{MNQ} = \int_{M}^{N} \mathbf{F} \cdot d\mathbf{r} + \int_{N}^{Q} \mathbf{F} \cdot d\mathbf{r} $$ Check if this integral equals $ \frac{\pi}{2} $.
-
Evaluate Work Along Circle Centered at (5,0) Calculate the work done when the particle moves along the circle of radius 1 m centered at (5,0). This path should also be evaluated using the line integral to see if $ W = 0 $.
-
Determine Conservativeness of the Force Field To check if the force is conservative, compute the curl of the force field: $$ \nabla \times \mathbf{F} = 0 $$ If the curl is not zero at any point, then the field is not conservative.
The incorrect options are B) work done in the open path MNQ is $\frac{\pi}{2}$ and D) $\mathbf{F}$ is conservative.
More Information
The given force field is not conservative due to a singularity at the origin, which affects the calculation of work. Option B indicates specific calculated work that may not hold with the correct method.
Tips
- Confusing conservative force with non-conservative due to overlooking singularities.
- Miscalculating the work done along paths due to incorrect parameterization or line integrals.
AI-generated content may contain errors. Please verify critical information