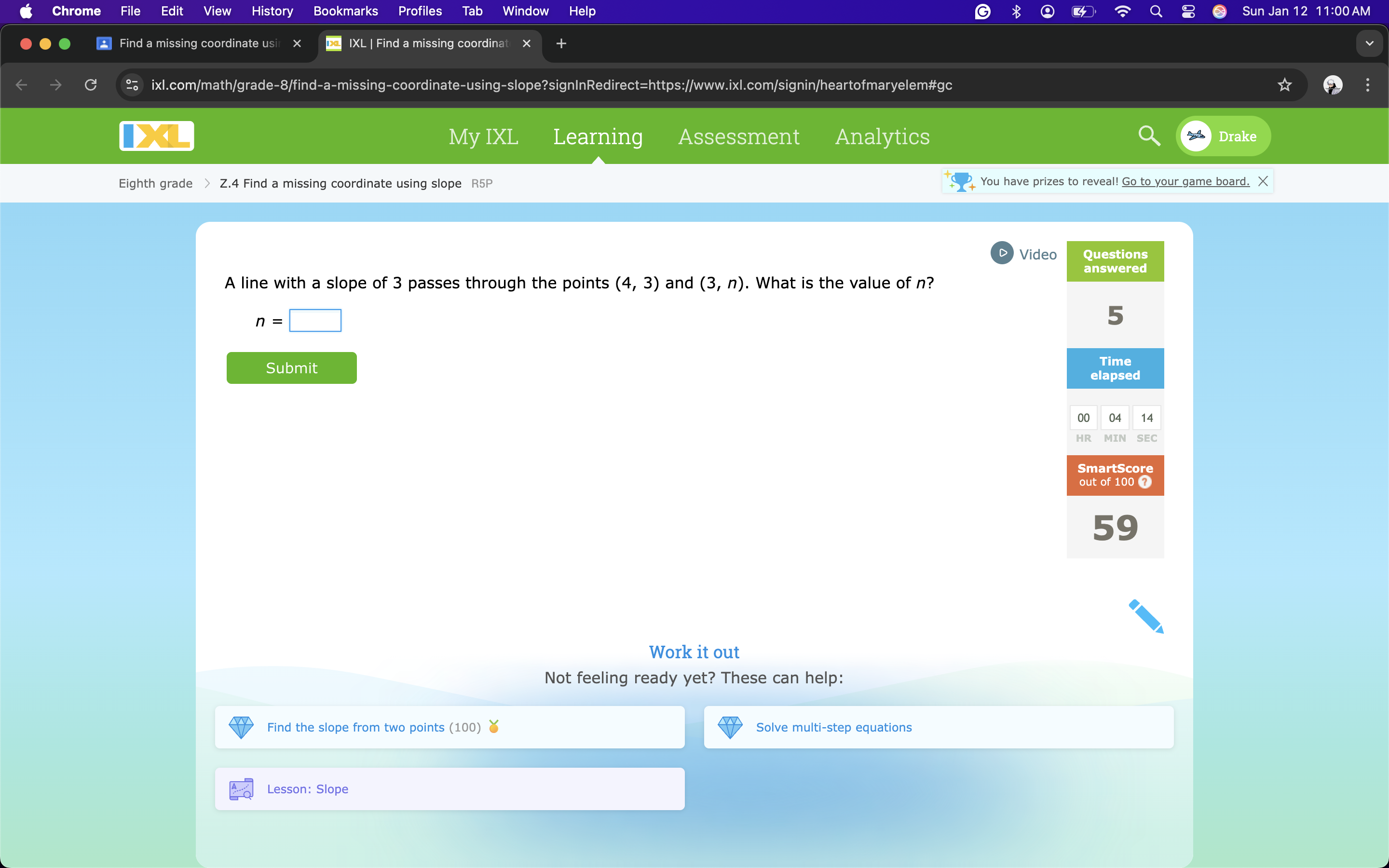
A line with a slope of 3 passes through the points (4, 3) and (3, n). What is the value of n?
Understand the Problem
The question is asking for the value of 'n' in the coordinate point (3, n) given that a line with a slope of 3 passes through the points (4, 3) and (3, n). To solve this, we will use the slope formula, which is the difference in y-values divided by the difference in x-values.
Answer
\( n = 0 \)
Answer for screen readers
The value of ( n ) is ( 0 ).
Steps to Solve
- Identify the slope formula The slope ($m$) of a line passing through two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by the formula:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
- Assign the points Here, we know:
- Point 1: $(4, 3)$ where $x_1 = 4$ and $y_1 = 3$
- Point 2: $(3, n)$ where $x_2 = 3$ and $y_2 = n$
- Plug the values into the slope formula Since the slope of the line is provided as $m = 3$, we substitute the values into the slope formula:
$$ 3 = \frac{n - 3}{3 - 4} $$
- Simplify the equation Calculate the denominator:
$$ 3 - 4 = -1 $$
So the equation becomes:
$$ 3 = \frac{n - 3}{-1} $$
- Solve for 'n' Multiply both sides by $-1$ to eliminate the fraction:
$$ -3 = n - 3 $$
Now, add 3 to both sides:
$$ -3 + 3 = n $$
Thus,
$$ n = 0 $$
The value of ( n ) is ( 0 ).
More Information
The value of ( n ) represents the y-coordinate of the point (3, n) on the line with a slope of 3 passing through (4, 3). By using the slope formula, we determined the missing coordinate necessary for defining the line.
Tips
- Forgetting to substitute correctly: Ensure all values are plugged in accurately.
- Sign errors: Be cautious with positive and negative signs when simplifying the equations.
AI-generated content may contain errors. Please verify critical information