A integral \int_{3}^{+\infty} \frac{dx}{x^4 \sqrt{x^2 - 4}} converge e seu valor é:
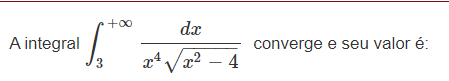
Understand the Problem
A questão está perguntando sobre a convergência da integral de uma função específica e quer saber o valor dessa integral desde 3 até o infinito. Essa é uma questão típica de cálculo envolvendo integrais impróprias.
Answer
A integral converge e seu valor é $\frac{1}{72}$.
Answer for screen readers
O valor da integral é $\frac{1}{72}$.
Steps to Solve
- Verificar a convergência da integral
Para determinar se a integral converge, consideramos a função integranda:
$$ f(x) = \frac{1}{x^4 \sqrt{x^2 - 4}} $$
Para $x$ grande (tendendo ao infinito), podemos aproximar a função:
$$ f(x) \approx \frac{1}{x^4 \sqrt{x^2}} = \frac{1}{x^4 x} = \frac{1}{x^5} $$
A integral de $\frac{1}{x^5}$ é conhecida e converge, já que
$$ \int \frac{1}{x^5} , dx $$
é uma integral imprópria convergente.
- Calcular a integral
Agora vamos calcular a integral imprópria:
$$ I = \int_{3}^{+\infty} \frac{dx}{x^4 \sqrt{x^2 - 4}} $$
Fazemos a substituição:
$$ \sqrt{x^2 - 4} = u $$
Logo,
$$ x^2 = u^2 + 4 $$
e, derivando,
$$ 2x , dx = 2u , du \Rightarrow dx = \frac{u , du}{\sqrt{u^2 + 4}} $$
Os limites da integral se transformam: quando $x = 3$, $u = \sqrt{3^2 - 4} = \sqrt{5}$. Quando $x \to \infty$, $u \to \infty$.
- Substituir na integral
Substituindo na integral:
$$ I = \int_{\sqrt{5}}^{+\infty} \frac{u , du}{(u^2 + 4)^{2} \sqrt{u^2}} $$
Simplificando, temos:
$$ I = \int_{\sqrt{5}}^{+\infty} \frac{du}{(u^2 + 4)^{2}} $$
- Calcular a nova integral
Agora vamos calcular a integral:
$$ I = \left[ -\frac{1}{8(u^2 + 4)} \right]_{\sqrt{5}}^{+\infty} $$
O limite superior vai a 0 assim que $u$ tende ao infinito:
$$ I = 0 - \left(-\frac{1}{8(\sqrt{5}^2 + 4)}\right) = \frac{1}{8(5 + 4)} = \frac{1}{8 \cdot 9} = \frac{1}{72} $$
O valor da integral é $\frac{1}{72}$.
More Information
A integral que foi avaliada é um exemplo clássico de integral imprópria, e a técnica de substituição e análise de comportamento assintótico são comuns na resolução desse tipo de problema em cálculo.
Tips
- Não verificar a convergência: É importante sempre verificar se a integral é convergente antes de calculá-la.
- Erros na substituição: Cuidar ao fazer substituições; é crucial que todos os limites e variáveis sejam corretamente ajustados.
AI-generated content may contain errors. Please verify critical information