A integral ∫₃^{+∞} rac{dx}{x^{4} ext{√{x^{2} - 4}}} converge e seu valor é:
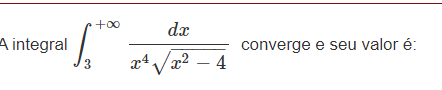
Understand the Problem
A questão está pedindo para calcular o valor da integral definida de um limite, avaliando se ela converge e qual é seu valor.
Answer
A integral converge e seu valor é $\frac{1}{324}$.
Answer for screen readers
A integral converge e seu valor é $$ \frac{1}{324} $$
Steps to Solve
-
Análise da integral A integral a ser avaliada é $$ \int_3^{+\infty} \frac{dx}{x^{4} \sqrt{x^{2} - 4}} $$ Primeiro, verificamos se a integral converge quando $x$ tende a $+\infty$.
-
Determinação do comportamento assintótico Para valores grandes de $x$, podemos aproximar $$ \sqrt{x^{2} - 4} \approx \sqrt{x^{2}} = x $$ Assim, a integral se torna $$ \int_3^{+\infty} \frac{dx}{x^{4} x} = \int_3^{+\infty} \frac{dx}{x^{5}} $$
-
Cálculo da integral Calculamos a integral $$ \int \frac{dx}{x^{5}} = -\frac{1}{4x^{4}} $$ Agora, avaliamos os limites da integral definida de 3 a $+\infty$: $$ \left[-\frac{1}{4x^{4}}\right]_{3}^{+\infty} $$
-
Avaliação dos limites Calculamos os limites:
- Para $x \to +\infty$: $-\frac{1}{4x^{4}} \to 0$
- Para $x = 3$: $-\frac{1}{4(3^{4})} = -\frac{1}{324}$
Portanto, a integral converge para: $$ 0 - \left(-\frac{1}{324}\right) = \frac{1}{324} $$
A integral converge e seu valor é $$ \frac{1}{324} $$
More Information
Esta integral é um exemplo de integral imprópria que converge. É importante reconhecer o comportamento de funções em limites extremos para determinar a convergência. Essa técnica é fundamental em cálculo integral.
Tips
- Não aplicar adequadamente a análise assintótica para $x$ muito grande, o que pode levar a conclusões incorretas sobre a convergência da integral.
- Esquecer de avaliar o limite na parte superior adequadamente, resultando em erros no valor final.
AI-generated content may contain errors. Please verify critical information