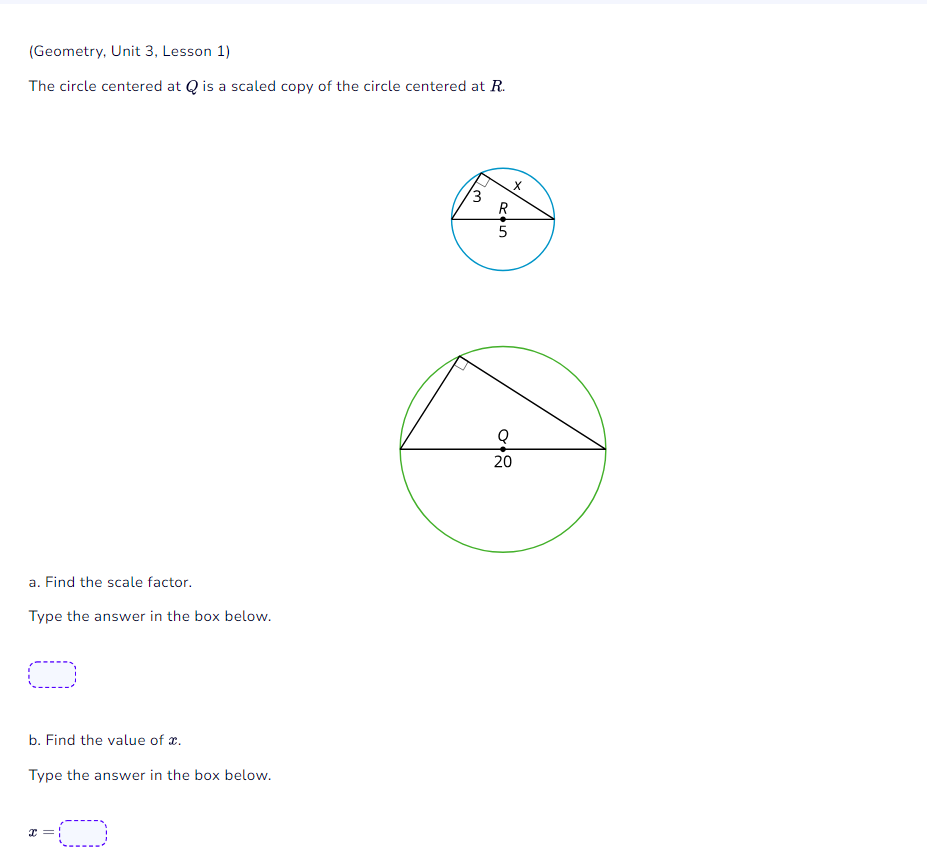
a. Find the scale factor. b. Find the value of x.

Understand the Problem

The question involves finding the scale factor between two circles and determining the value of the variable x based on the given dimensions of the circles. It requires calculations related to the properties of similar shapes in geometry.

Answer

a. $\frac{12}{5}$ b. $3$

Steps to Solve

Identify the radii and setup the ratio

The radius of the smaller circle at ( R ) is represented as ( R ) and the radius of the larger circle at ( Q ) is given as ( 20 ). The smaller circle's dimensions have a radius ( \frac{3}{5} R ).

Find the scale factor

The scale factor ( k ) between two similar figures is calculated by the ratio of their corresponding dimensions (radii in this case). Thus, we have:

$$ k = \frac{\text{Radius of larger circle}}{\text{Radius of smaller circle}} = \frac{20}{R} $$

Relate the radius ( R ) to the smaller circle dimensions

From the smaller circle, we know:

$$ \frac{3}{5} R = 5 $$

To find ( R ), we rearrange this equation:

$$ R = 5 \times \frac{5}{3} = \frac{25}{3} $$

Substitute to find the scale factor

Now substitute ( R ) back into the scale factor equation:

$$ k = \frac{20}{\frac{25}{3}} = 20 \times \frac{3}{25} = \frac{60}{25} = \frac{12}{5} $$

Determine the value of ( x )

Using the relationship between ( x ) and ( R ) again from the dimensions of the smaller circle, we have:

$$ \frac{x}{5} = \frac{3}{5} $$

To determine ( x ):

$$ x = 3 $$

a. Scale factor: $\frac{12}{5}$

b. Value of ( x ): $3$

More Information

The scale factor tells us how many times larger the larger circle is compared to the smaller one. The value of ( x ) corresponds to the necessary dimension in the smaller circle based on its scaling factor.

Tips

Confusing the scale factor with a difference in dimensions rather than a ratio.
Misinterpreting the relationship between the dimensions while setting up equations.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!