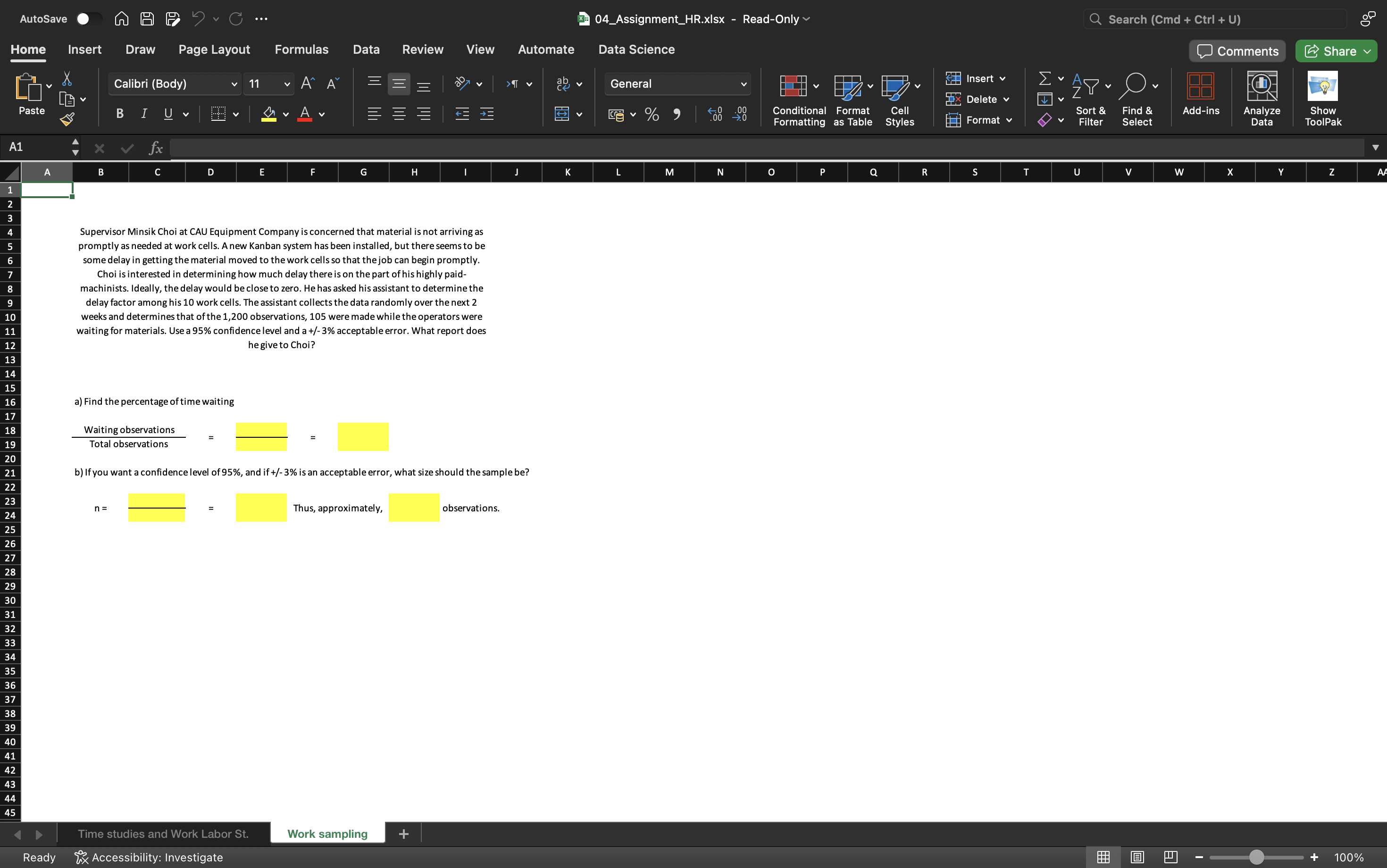
a) Find the percentage of time waiting. b) If you want a confidence level of 95%, and if +/-3% is an acceptable error, what size should the sample be?

Steps to Solve

1. Calculate the Percentage of Time Waiting

To find the percentage of time the operators were waiting for materials, use the formula:

$$ \text{Percentage} = \left( \frac{\text{Waiting observations}}{\text{Total observations}} \right) \times 100 $$

Here, the waiting observations are 105 and the total observations are 1200.

$$ \text{Percentage} = \left( \frac{105}{1200} \right) \times 100 $$

2. Determine the Sample Size Needed

To calculate the required sample size for a 95% confidence level with an acceptable error of ±3%, use the formula:

$$ n = \left( \frac{Z^2 \cdot p \cdot (1-p)}{E^2} \right) $$

Where:

• ( Z ) is the Z-score for the confidence level (1.96 for 95%)
• ( p ) is the estimated proportion (from part a, in decimal form)
• ( E ) is the margin of error (0.03 for ±3%)

Calculate ( p ):

$$ p = \frac{105}{1200} = 0.0875 $$

Next, substitute the values into the sample size formula:

$$ n = \left( \frac{(1.96)^2 \cdot 0.0875 \cdot (1 - 0.0875)}{(0.03)^2} \right) $$

3. Calculate the Sample Size

First, compute ( (1 - p) ):

$$ 1 - p = 1 - 0.0875 = 0.9125 $$

Now plug everything into the sample size formula:

$$ n = \left( \frac{3.8416 \cdot 0.0875 \cdot 0.9125}{0.0009} \right) $$

Finally, calculate ( n ) to find the required sample size.