A = cos²(10°) + (cos²(20°) + (cos²(28°)) - x sin(70°)
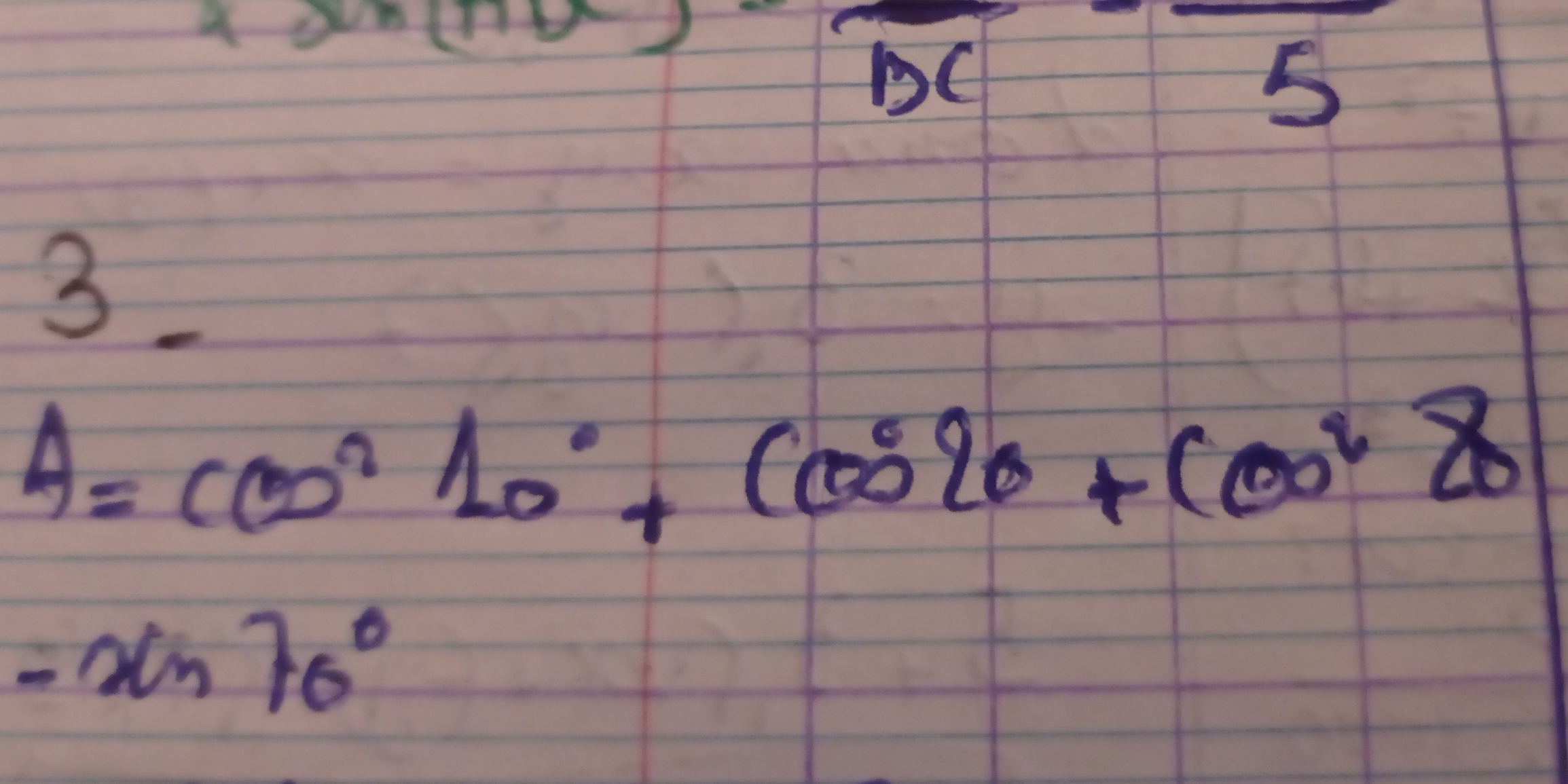
Understand the Problem
The question involves a mathematical expression that appears to involve trigonometric functions, specifically cosine, along with an angle measurement. The user is likely seeking assistance in simplifying or solving this expression.
Answer
$$ A \approx 2.6323 - x(0.9397) $$
Answer for screen readers
The simplified equation is: $$ A \approx 2.6323 - x(0.9397) $$
Steps to Solve
-
Identify the components of the equation The equation given is: $$ A = \cos^2(10°) + (\cos^2(20°) + \cos^2(28°)) - x \sin(70°) $$
-
Simplify the cosine squares We can evaluate $\cos^2(10°)$, $\cos^2(20°)$, and $\cos^2(28°)$ using known trigonometric values or a calculator. Here we use the approximations:
- $\cos(10°) \approx 0.9848 \Rightarrow \cos^2(10°) \approx 0.9698$
- $\cos(20°) \approx 0.9397 \Rightarrow \cos^2(20°) \approx 0.8830$
- $\cos(28°) \approx 0.8829 \Rightarrow \cos^2(28°) \approx 0.7795$
-
Perform the calculations Now substitute these values into the equation: $$ A \approx 0.9698 + (0.8830 + 0.7795) - x \sin(70°) $$
-
Calculate the sine of 70 degrees Using the known value:
- $\sin(70°) \approx 0.9397$
-
Combine the results Combine the cosine squares: $$ A \approx 0.9698 + 0.8830 + 0.7795 - x(0.9397) $$ $$ A \approx 2.6323 - x(0.9397) $$
-
Solve for x If a specific value for $A$ is given, set up the equation: $$ A = 2.6323 - x(0.9397) $$ Then solve for $x$.
The simplified equation is: $$ A \approx 2.6323 - x(0.9397) $$
More Information
This equation represents a function of $A$ dependent on the variable $x$. The cosine and sine values are approximated for angles in degrees, which are commonly used in trigonometric problems.
Tips
Common mistakes include:
- Confusing sine and cosine values.
- Incorrectly squaring the cosine values or miscalculating the results.
- Not using degrees when inputting values into a calculator.
AI-generated content may contain errors. Please verify critical information