A container in R^3 has the shape of the cube given by 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1. A plate is placed in the container in such a way that it occupies that portion of the plane x... A container in R^3 has the shape of the cube given by 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1. A plate is placed in the container in such a way that it occupies that portion of the plane x + y + z = 1 that lies on the cubical container. If the container is heated so that the temperature at each point (x, y, z) is given by T(x, y, z) = 4 - 2x^2 - y^2 - z^2 in hundreds of degrees Celsius, what are the hottest and coldest points on the plate? Use Lagrange's multipliers method to identify all the critical points in the interior of the plate and be certain to examine the plate boundaries.
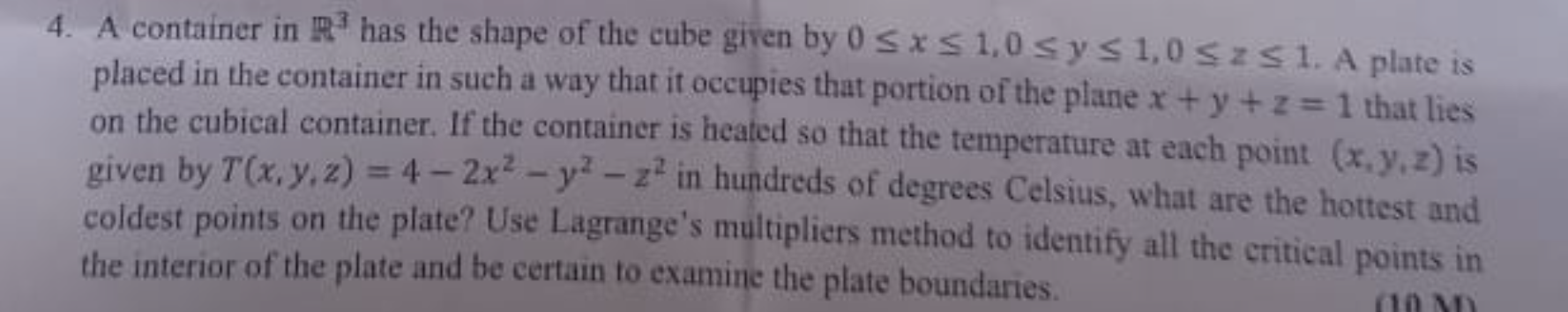
Understand the Problem
The question is asking to determine the hottest and coldest points on a plate situated within a cubical container and heated according to a specific temperature function. Lagrange's multipliers need to be used to identify critical points while considering the boundaries of the plate.
Answer
Hottest point: $ \left( \frac{1}{5}, \frac{2}{5}, \frac{2}{5} \right) $, Temperature: $ 3.6 $; Coldest point: $ (1, 0, 0) $, Temperature: $ 2 $.
Answer for screen readers
The hottest point on the plate is at $ \left( \frac{1}{5}, \frac{2}{5}, \frac{2}{5} \right) $ with a temperature of $ 3.6 $.
The coldest points on the plate are at $ (1, 0, 0) $ with $ T = 2 $.
Steps to Solve
-
Define the temperature function and constraint
The temperature function is given by $$ T(x, y, z) = 4 - 2x^2 - y^2 - z^2 $$ The constraint is the plane defined by the equation $$ g(x, y, z) = x + y + z - 1 = 0 $$
-
Set up Lagrange's multipliers
We need to find the gradient of the temperature function and the gradient of the constraint:
-
Gradient of $T$: $$ \nabla T = \left( -4x, -2y, -2z \right) $$
-
Gradient of $g$: $$ \nabla g = (1, 1, 1) $$
According to Lagrange's method, we set $$ \nabla T = \lambda \nabla g $$ This gives us the system of equations: $$ -4x = \lambda $$ $$ -2y = \lambda $$ $$ -2z = \lambda $$
-
-
Solve for $x$, $y$, and $z$ in terms of $\lambda$
From the equations, we can express: $$ x = -\frac{\lambda}{4} $$ $$ y = -\frac{\lambda}{2} $$ $$ z = -\frac{\lambda}{2} $$
-
Substitute in the constraint
Substitute these expressions into the constraint $x + y + z = 1$: $$ -\frac{\lambda}{4} - \frac{\lambda}{2} - \frac{\lambda}{2} = 1 $$ This simplifies to: $$ -\frac{\lambda}{4} - \frac{2\lambda}{4} - \frac{2\lambda}{4} = 1 $$ Adding gives: $$ -\frac{5\lambda}{4} = 1 $$
Thus, solving for $\lambda$: $$ \lambda = -\frac{4}{5} $$
-
Determine $x$, $y$, and $z$
Substitute $\lambda$ back to find $x$, $y$, and $z$: $$ x = \frac{1}{5}, \quad y = \frac{2}{5}, \quad z = \frac{2}{5} $$
-
Compute the temperature at critical point
Now substitute these values into the temperature function: $$ T\left(\frac{1}{5}, \frac{2}{5}, \frac{2}{5}\right) = 4 - 2\left(\frac{1}{5}\right)^2 - \left(\frac{2}{5}\right)^2 - \left(\frac{2}{5}\right)^2 $$
Calculate step by step: $$ T = 4 - 2\left(\frac{1}{25}\right) - \frac{4}{25} - \frac{4}{25} $$ $$ = 4 - \frac{2}{25} - \frac{4}{25} - \frac{4}{25} $$ $$ = 4 - \frac{10}{25} $$ $$ = 4 - \frac{2}{5} = 4 - 0.4 = 3.6 $$
-
Evaluate temperature on the boundaries of the plate
The plate boundaries are where one of the variables is at its extreme values (0 or 1). We can check combinations of $(x, y, z)$ that satisfy $x + y + z = 1$:
- $(1, 0, 0)$
- $(0, 1, 0)$
- $(0, 0, 1)$
- $(1, 0, 0)$ gives $T(1, 0, 0) = 4 - 2(1^2) - 0 - 0 = 2$
- $(0, 1, 0)$ gives $T(0, 1, 0) = 4 - 0 - 1 - 0 = 3$
- $(0, 0, 1)$ gives $T(0, 0, 1) = 4 - 0 - 0 - 1 = 3$
-
Compare all temperatures
Finally, comparing:
- Critical point: $T\left(\frac{1}{5}, \frac{2}{5}, \frac{2}{5}\right) = 3.6$
- Boundaries: $T(1, 0, 0) = 2$, $T(0, 1, 0) = 3$, $T(0, 0, 1) = 3$
The hottest point on the plate is at $ \left( \frac{1}{5}, \frac{2}{5}, \frac{2}{5} \right) $ with a temperature of $ 3.6 $.
The coldest points on the plate are at $ (1, 0, 0) $ with $ T = 2 $.
More Information
The temperature function was analyzed using the method of Lagrange multipliers, which allowed us to find critical points under a constraint. The discovered points revealed the locations of maximum and minimum temperatures on the plate.
Tips
- Confusing the constraints when evaluating boundaries.
- Failing to check all boundaries of the defined region.
- Incorrectly calculating temperature values at critical points.
AI-generated content may contain errors. Please verify critical information