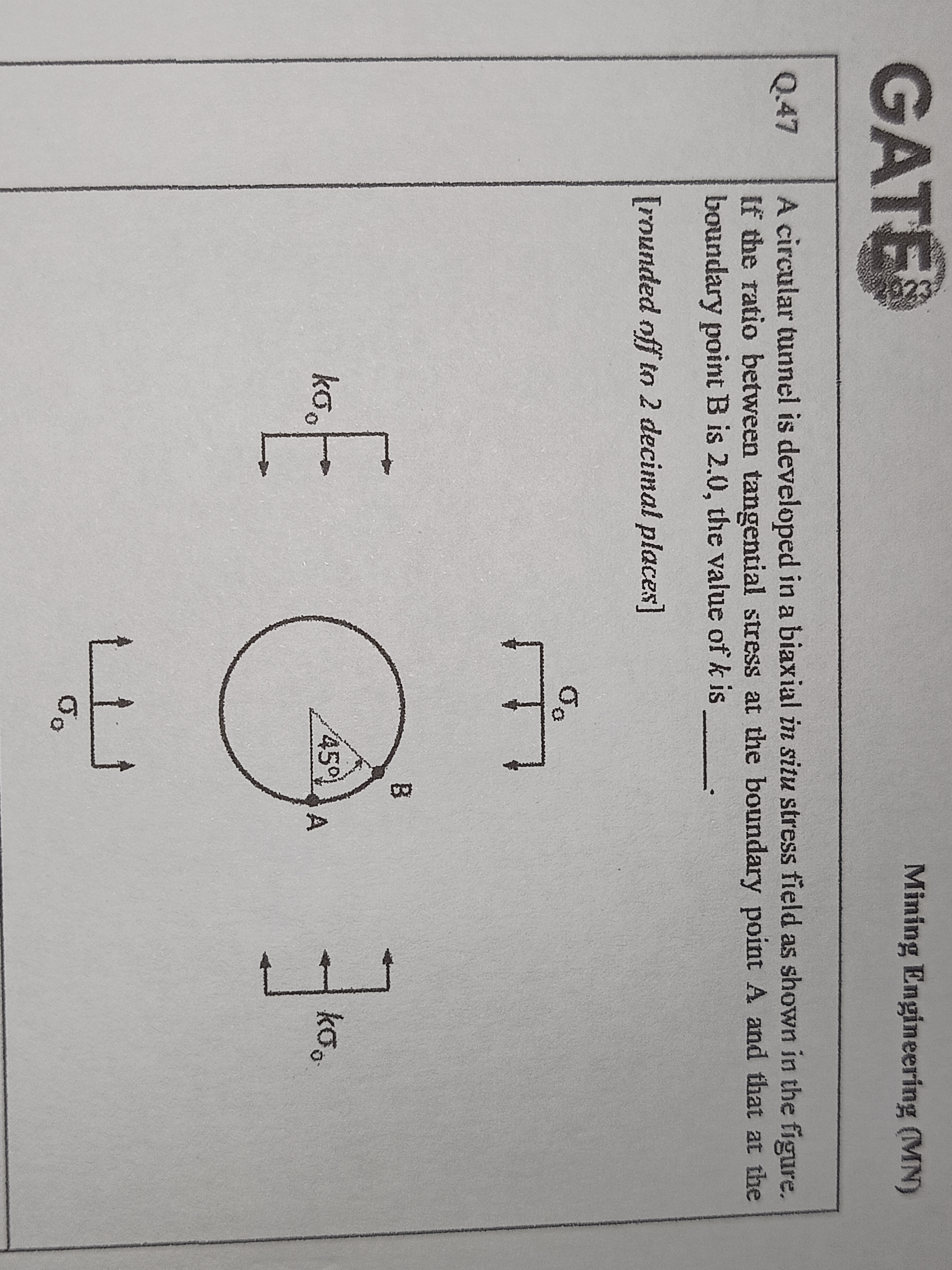
A circular tunnel is developed in a biaxial stress field as shown in the figure. If the ratio between tangential stresses at the boundary point B is 2.0, what is the value of sigma... A circular tunnel is developed in a biaxial stress field as shown in the figure. If the ratio between tangential stresses at the boundary point B is 2.0, what is the value of sigma at A? Read more

Steps to Solve

1. Identify Given Data

The problem provides the following data:

• At point A:

  • Normal stress, $\sigma_A = \sigma_0$
  • Lateral stress, $\sigma_{\theta A} = k_0 \sigma_0$

• At point B:

  • Angle from horizontal at A to B is $45^\circ$.

• Ratio of tangential stress at point B to that at point A is given as $R = 2.0$.

2. Relate Stresses at Points A and B

The relationship between the stresses can be expressed using Mohr’s Circle. At point A, the normal $\sigma_A$ and tangential stresses can be related to point B:

Using the equations of transformation of stress:

$$ \sigma_B = \sigma_A \cos^2(\theta) + \sigma_{\theta A} \sin^2(\theta) $$

$$ \tau_B = \frac{(\sigma_A - \sigma_{\theta A})}{2} \sin(2\theta) $$

3. Calculate Stresses at Point B

Since $\theta = 45^\circ$, the following values apply:

• $\cos(45^\circ) = \sin(45^\circ) = \frac{\sqrt{2}}{2}$

Insert these values into the equations for stress:

For normal stress at point B:

$$ \sigma_B = \sigma_0 \left(\frac{\sqrt{2}}{2}\right)^2 + (k_0 \sigma_0) \left(\frac{\sqrt{2}}{2}\right)^2 $$ $$ \sigma_B = \sigma_0 \cdot \frac{1}{2} + k_0 \sigma_0 \cdot \frac{1}{2} $$ $$ \sigma_B = \frac{(1 + k_0)}{2} \sigma_0 $$

For tangential stress at point B:

$$ \tau_B = \frac{(\sigma_A - \sigma_{\theta A})}{2} \sin(90^\circ) $$ $$ \tau_B = \frac{(\sigma_0 - k_0 \sigma_0)}{2} = \frac{(1-k_0)}{2} \sigma_0 $$

4. Relate Stresses Using Given Ratio

Now, we use the given ratio $R = \frac{\tau_B}{\tau_A} = 2.0$:

Let $\tau_A = \tau_A$, then:

$$ 2.0 = \frac{\tau_B}{\tau_A} $$ $$ \tau_A = \tau_A $$

Substituting $\tau_B$ into the equation gives:

$$ 2.0 = \frac{\frac{(1-k_0)}{2} \sigma_0}{\tau_A} $$

This means we need to express $\tau_A$ in terms of known quantities. Solve for $k_0$.

5. Solve for $k_0$

Using the derived equations and substituting values of known stresses, we can rearranged to find $k_0$:

Rearranging leads to equations that can be solved for $k_0$, specifically relating to the given ratio.

6. Final Calculations

Calculate final values step using numerical or symbolic methods for solving $k_0$ and rounded value to desired decimal places.