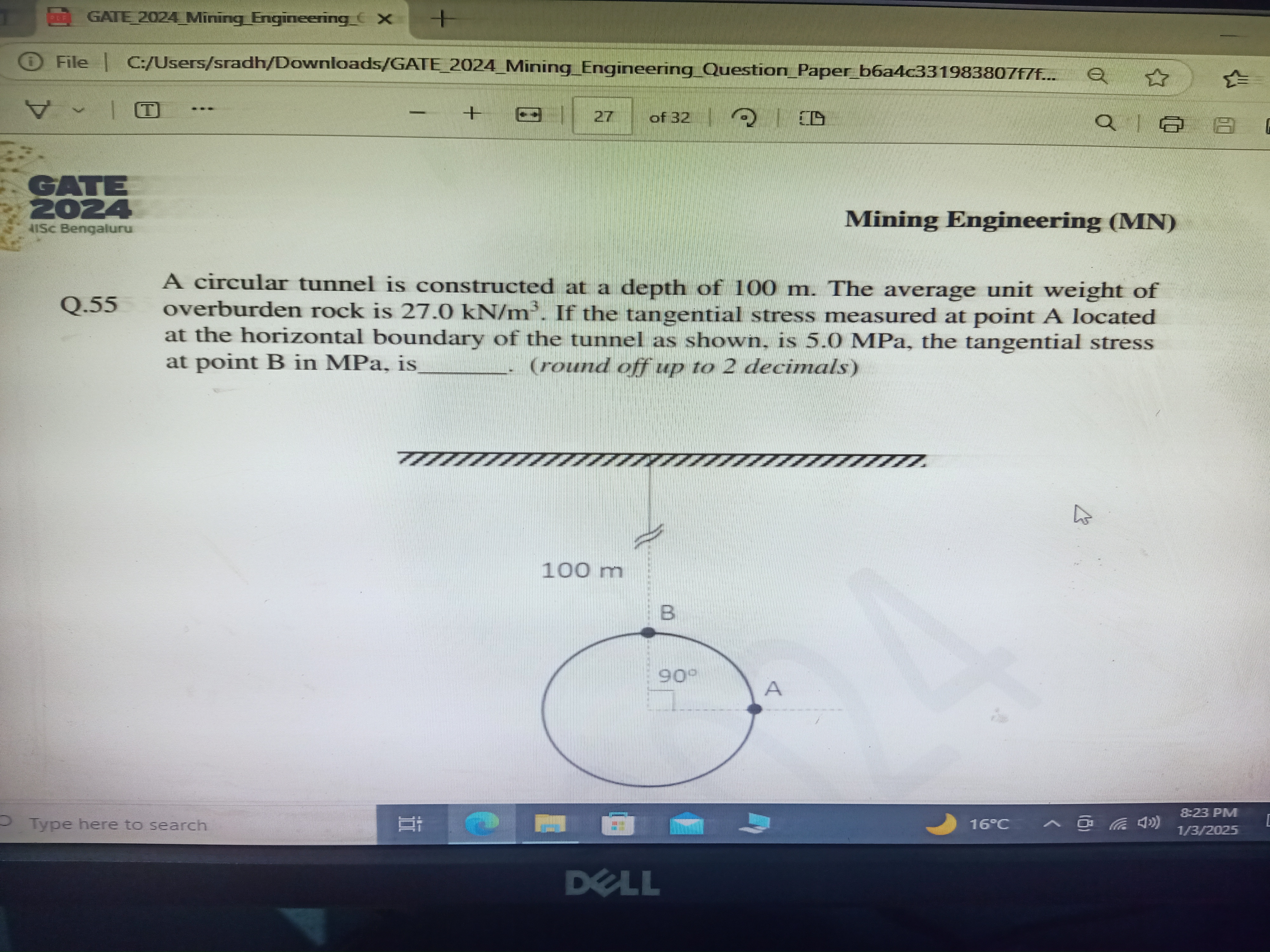
A circular tunnel is constructed at a depth of 100 m. The average unit weight of overburden rock is 27.0 kN/m³. If the tangential stress measured at point A is 5.0 MPa, what is the... A circular tunnel is constructed at a depth of 100 m. The average unit weight of overburden rock is 27.0 kN/m³. If the tangential stress measured at point A is 5.0 MPa, what is the tangential stress at point B in MPa? (round off to 2 decimals)
Understand the Problem
The question is asking to calculate the tangential stress at point B of a circular tunnel, given certain parameters, including the depth, the average unit weight of the overburden rock, and the tangential stress at point A. The answer needs to be rounded to two decimal places.
Answer
$18.50 \, \text{MPa}$
Answer for screen readers
The tangential stress at point B is $18.50 , \text{MPa}$.
Steps to Solve
- Calculate Effective Stress Due to Depth
The total vertical stress at depth can be calculated using the formula:
$$ \sigma_v = \gamma \cdot h $$
where:
- $\gamma$ = unit weight of rock = 27.0 kN/m³
- $h$ = depth = 100 m
Plugging in the values:
$$ \sigma_v = 27.0 , \text{kN/m}^3 \times 100 , \text{m} = 2700 , \text{kN/m}^2 = 27.0 , \text{MPa} $$
- Determine the Change in Tangential Stress
The change in tangential stress from point A to point B can be approximated based on the depth as:
$$ \Delta \sigma_t = \frac{\sigma_v}{2} $$
Using the calculated vertical stress:
$$ \Delta \sigma_t = \frac{27.0}{2} = 13.5 , \text{MPa} $$
- Calculate the Tangential Stress at Point B
To find the tangential stress at point B, add the change in stress to the tangential stress at point A:
$$ \sigma_t(B) = \sigma_t(A) + \Delta \sigma_t $$
Substituting the known values:
$$ \sigma_t(B) = 5.0 , \text{MPa} + 13.5 , \text{MPa} = 18.5 , \text{MPa} $$
- Round the Result
Finally, round the result to two decimal places:
$$ \sigma_t(B) = 18.50 , \text{MPa} $$
The tangential stress at point B is $18.50 , \text{MPa}$.
More Information
The calculation demonstrates how stress changes in a circular tunnel due to depth. Understanding these geomechanical principles is critical in mining engineering and tunnel construction.
Tips
- Forgetting to convert units (e.g., kN/m² to MPa).
- Incorrectly calculating the change in tangential stress. Remember to use the vertical stress correctly.
AI-generated content may contain errors. Please verify critical information