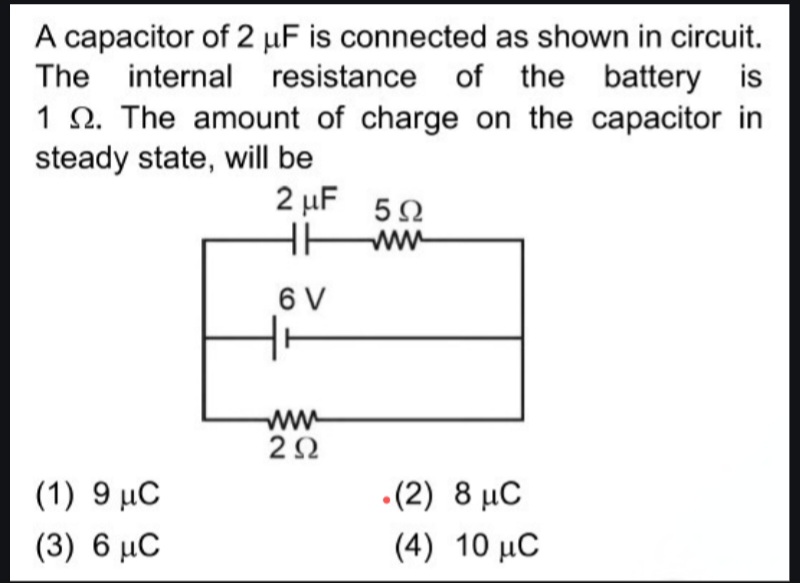
A capacitor of 2 µF is connected as shown in circuit. The internal resistance of the battery is 1 Ω. The amount of charge on the capacitor in steady state will be?

Steps to Solve

1. Identify the circuit and components

In the given circuit, we have a capacitor, resistors, and a battery. The capacitor value is $2 , \mu F$ and the resistors are $5 , \Omega$ and $2 , \Omega$ with an internal resistance of $1 , \Omega$. The effective resistance in series with the capacitor can be calculated as:
$$ R_{total} = 5 , \Omega + 2 , \Omega + 1 , \Omega = 8 , \Omega $$

2. Calculate the total current in the circuit

Using Ohm's law, the current $I$ flowing through the circuit can be calculated by:
$$ I = \frac{V}{R_{total}} = \frac{6 , V}{8 , \Omega} = 0.75 , A $$

3. Determine the voltage across the capacitor

Since the capacitor is in steady state, the voltage across it can be found using the formula for charge on a capacitor:
$$ V_C = I \times R_{equiv} $$
Where $R_{equiv}$ is the total resistance in series with the capacitor. We can find this by taking the total voltage drop across resistors. The total resistance is $8 , \Omega$, hence:
$$ V_C = I \times (2 , \Omega + 5 , \Omega) = 0.75 , A \times 7 , \Omega = 5.25 , V $$

4. Calculate the charge on the capacitor

Now, using the capacitance formula: $$ Q = C \times V_C $$
Where ( C = 2 , \mu F ), we convert capacitance to farads: ( 2 , \mu F = 2 \times 10^{-6} F ). So:
$$ Q = 2 \times 10^{-6} F \times 5.25 , V = 10.5 \times 10^{-6} , C = 10.5 , \mu C $$

5. Final approximation and values

Since the options provided are discrete values, we need to round to the closest presented answer, which is $10 , \mu C$.