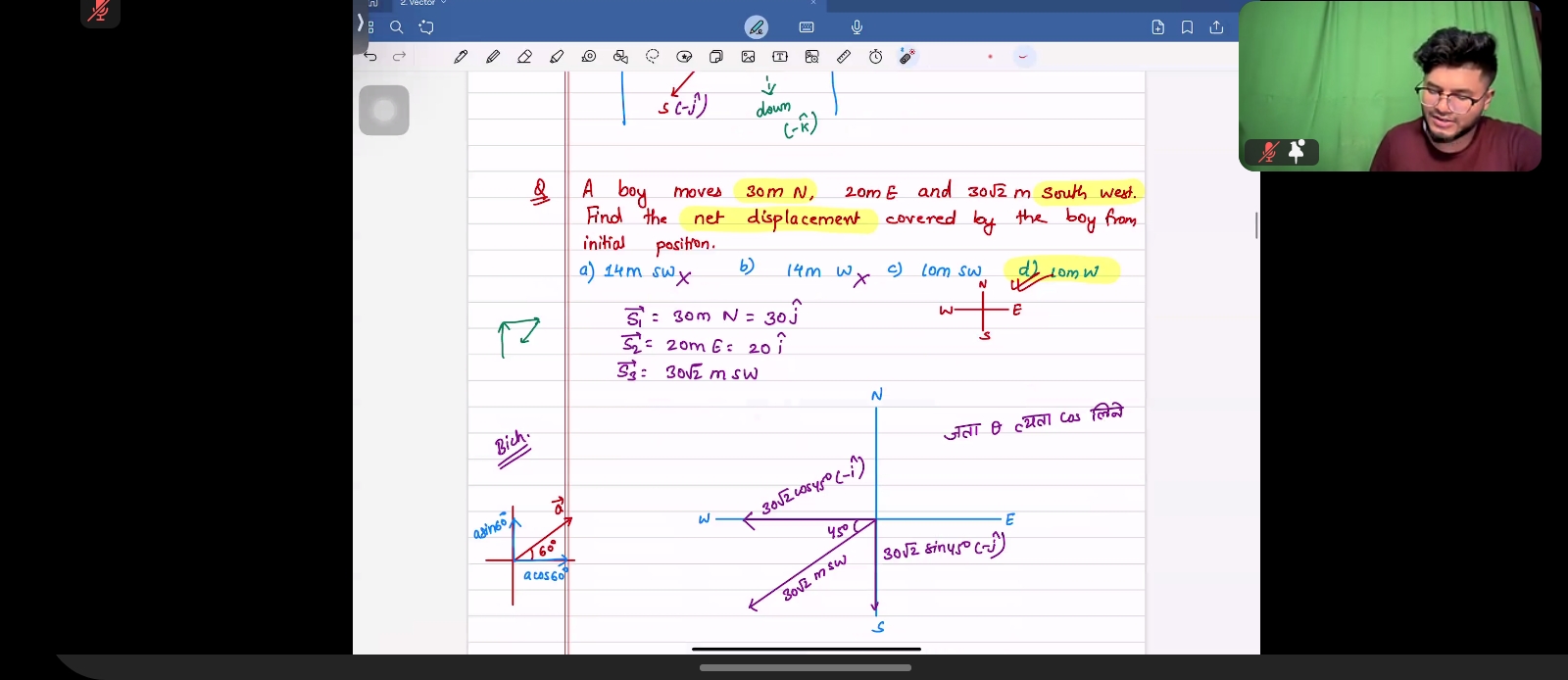
A boy moves 30 m North, 20 m East, and 30√2 m South West. Find the net displacement covered by the boy from his initial position.

Steps to Solve

1. Identify the Movements and Their Directions

The boy's movements are as follows:

• 30 m North: This can be represented as a vector $\mathbf{S_1} = 30\mathbf{j}$.
• 20 m East: This can be represented as a vector $\mathbf{S_2} = 20\mathbf{i}$.
• 30√2 m Southwest: This needs to be broken down into its components. Since southwest is at a 45-degree angle from both the south and west axes, we find the components using trigonometry.

2. Calculate the Southwest Vector Components

For the vector $\mathbf{S_3} = 30\sqrt{2}\mathbf{m_{SW}}$, we resolve it into its x (west) and y (south) components:

• The angle for southwest is $135^\circ$ (45° from the negative x and y axes).

Calculating using cosine and sine:

• West component: $$ S_{3x} = 30\sqrt{2} \cos(45^\circ) = 30\sqrt{2} \cdot \frac{1}{\sqrt{2}} = 30 \text{ m} $$
• South component: $$ S_{3y} = 30\sqrt{2} \sin(45^\circ) = 30\sqrt{2} \cdot \frac{1}{\sqrt{2}} = 30 \text{ m} $$

Thus, we have: $$ \mathbf{S_3} = -30\mathbf{i} - 30\mathbf{j} $$

3. Combine All Displacement Vectors

Now sum all the vectors: $$ \mathbf{S_{net}} = \mathbf{S_1} + \mathbf{S_2} + \mathbf{S_3} $$

Plugging in the values: $$ \mathbf{S_{net}} = 30\mathbf{j} + 20\mathbf{i} - 30\mathbf{i} - 30\mathbf{j} $$

4. Simplify the Resultant Vector

Combining like terms: $$ \mathbf{S_{net}} = (20 - 30)\mathbf{i} + (30 - 30)\mathbf{j} = -10\mathbf{i} + 0\mathbf{j} $$

This results in: $$ \mathbf{S_{net}} = -10\mathbf{i} $$

5. Find the Net Displacement Magnitude

Since the net displacement vector is purely in the x-direction (west): $$ |\mathbf{S_{net}}| = 10 \text{ m} $$