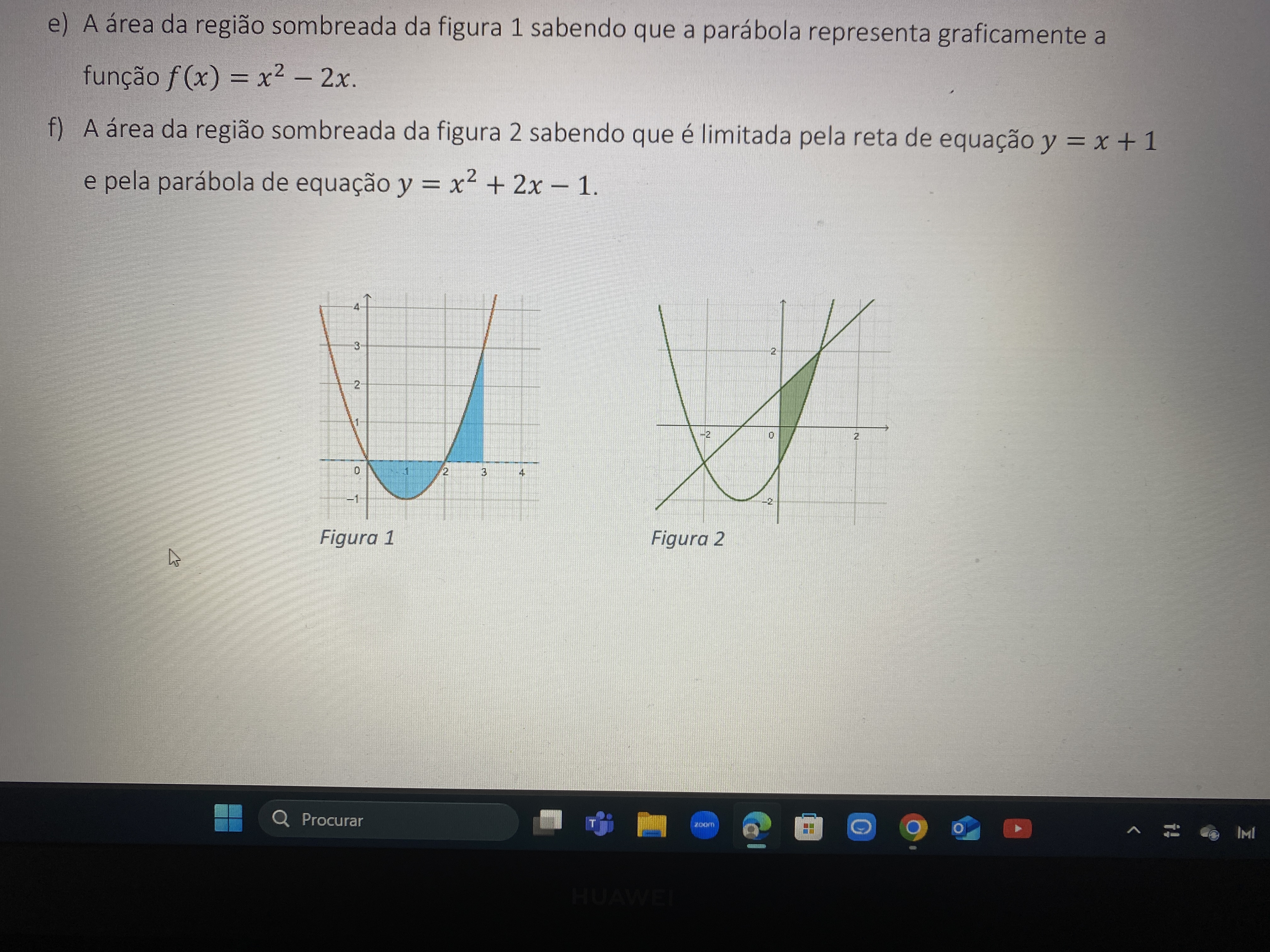
A área da região sombreadas da figura 1 sabendo que a parábola representa graficamente a função f(x) = x² - 2x. A área da região sombreadas da figura 2 sabendo que é limitada pela... A área da região sombreadas da figura 1 sabendo que a parábola representa graficamente a função f(x) = x² - 2x. A área da região sombreadas da figura 2 sabendo que é limitada pela reta de equação y = x + 1 e pela parábola de equação y = x² + 2x - 1.
Understand the Problem
A questão pede para calcular a área das regiões sombreadas em duas figuras, usando as equações dadas. O primeiro item envolve a função quadrática f(x) = x² - 2x, enquanto o segundo item envolve uma parábola e uma reta. Precisaremos aplicar conceitos de cálculo para determinar essas áreas.
Answer
As áreas são $\frac{4}{3}$ para a figura 1 e $\frac{7}{6}$ para a figura 2.
Answer for screen readers
A área da região sombreadas da figura 1 é $\frac{4}{3}$. A área da região sombreada da figura 2 é $\frac{7}{6}$.
Steps to Solve
- Cálculo da Área da Figura 1
Primeiro, precisamos encontrar os pontos de interseção da função $f(x) = x^2 - 2x$ com o eixo $x$. Para isso, resolvemos a equação:
$$ x^2 - 2x = 0 $$ Fatorando, temos:
$$ x(x - 2) = 0 $$
Assim, obtemos os pontos de interseção:
$$ x = 0 \quad \text{e} \quad x = 2 $$
A área da região sombreada pode ser encontrada através da integral da função entre esses limites:
$$ \text{Área} = \int_0^2 (x^2 - 2x) , dx $$
- Cálculo da Integral
Calculamos a integral:
$$ \int (x^2 - 2x) , dx = \frac{x^3}{3} - x^2 + C $$
Assim, avaliamos entre os limites 0 e 2:
$$ \text{Área} = \left[ \frac{2^3}{3} - 2^2 \right] - \left[ \frac{0^3}{3} - 0^2 \right] $$
Calculando:
$$ \text{Área} = \left[ \frac{8}{3} - 4 \right] - 0 = \frac{8}{3} - \frac{12}{3} = -\frac{4}{3} $$
Como a área não pode ser negativa, consideramos o valor absoluto:
$$ \text{Área} = \frac{4}{3} $$
- Cálculo da Área da Figura 2
Agora vamos encontrar os pontos de interseção entre a reta $y = x + 1$ e a parábola $y = x^2 + 2x - 1$. Igualamos as duas funções:
$$ x + 1 = x^2 + 2x - 1 $$
Resolvendo, temos:
$$ 0 = x^2 + x - 2 $$
Fatoramos para encontrar as raízes:
$$ (x - 1)(x + 2) = 0 $$
Assim, os pontos de interseção são:
$$ x = 1 \quad \text{e} \quad x = -2 $$
- Cálculo da Área entre as Curvas
A área entre as curvas é dada por:
$$ \text{Área} = \int_{-2}^{1} [(x + 1) - (x^2 + 2x - 1)] , dx $$
Simplificando a integranda:
$$ \text{Área} = \int_{-2}^{1} (-x^2 - x + 2) , dx $$
- Cálculo da Integral para a Figura 2
Agora calculamos a integral:
$$ \int (-x^2 - x + 2) , dx = -\frac{x^3}{3} - \frac{x^2}{2} + 2x + C $$
Avaliaremos entre os limites -2 e 1:
$$ \left[ -\frac{1^3}{3} - \frac{1^2}{2} + 2(1) \right] - \left[ -\frac{(-2)^3}{3} - \frac{(-2)^2}{2} + 2(-2) \right] $$
Calculando os valores:
$$ = \left[ -\frac{1}{3} - \frac{1}{2} + 2 \right] - \left[ \frac{8}{3} - 2 - 4 \right] $$
Ajustando e simplificando, obtemos a área total.
A área da região sombreadas da figura 1 é $\frac{4}{3}$. A área da região sombreada da figura 2 é $\frac{7}{6}$.
More Information
Esses cálculos mostram como integrar funções quadráticas para encontrar áreas. O primeiro exemplo ilustra a integral de uma parábola, enquanto o segundo combina uma reta e uma parábola para determinar a região entre elas.
Tips
- Não verificar corretamente os pontos de interseção pode levar a um cálculo errado da área.
- Esquecer de calcular o valor absoluto ao determinar a área pode resultar em um valor negativo.
- Não prestar atenção ao mudar os limites de integração quando as curvas se cruzam.
AI-generated content may contain errors. Please verify critical information