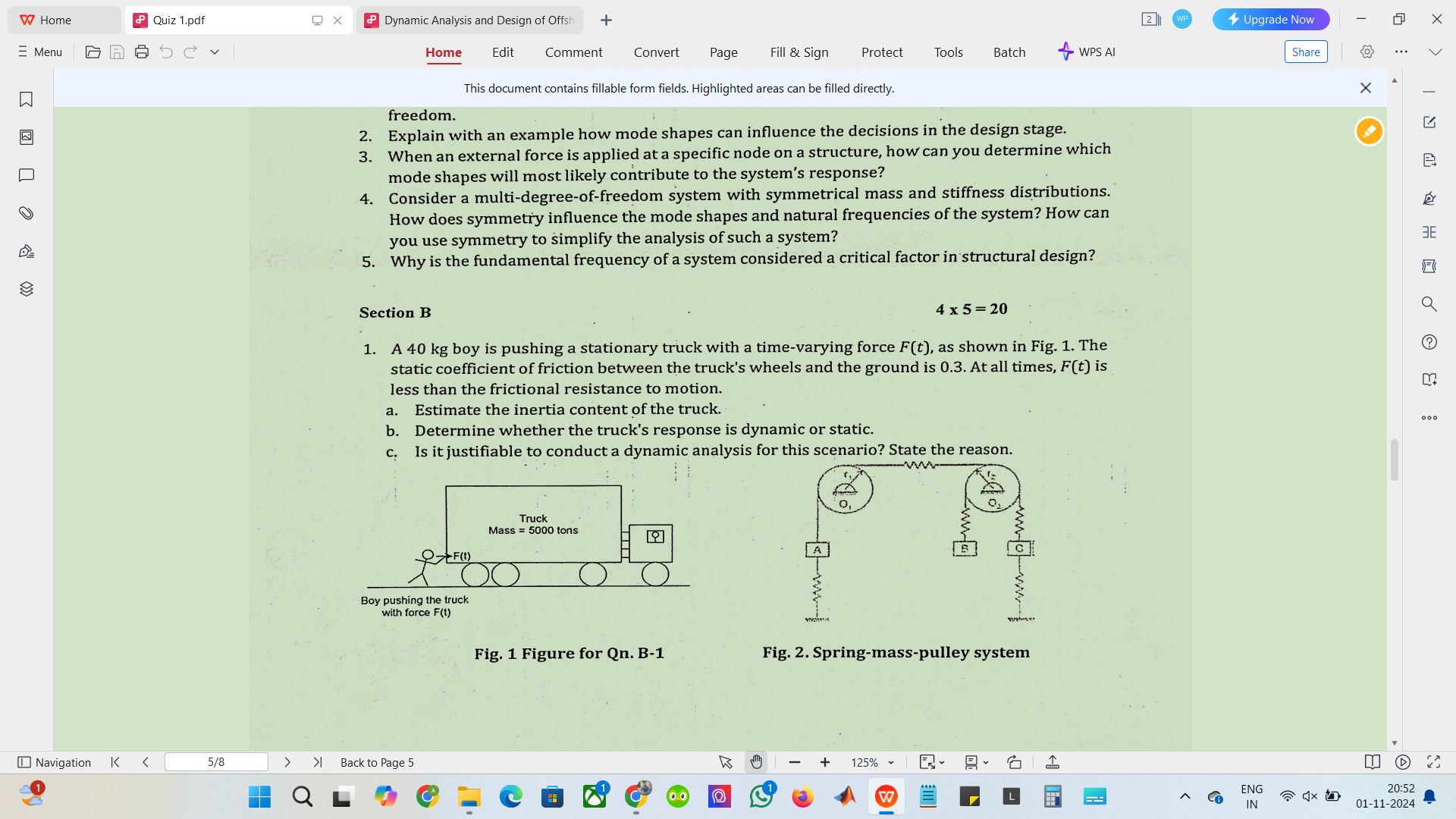
A 40 kg boy is pushing a stationary truck with a time-varying force F(t). The static coefficient of friction between the truck's wheels and the ground is 0.3. At all times, F(t) is... A 40 kg boy is pushing a stationary truck with a time-varying force F(t). The static coefficient of friction between the truck's wheels and the ground is 0.3. At all times, F(t) is less than the frictional resistance to motion. a. Estimate the inertia content of the truck. b. Determine whether the truck's response is dynamic or static. c. Is it justifiable to conduct a dynamic analysis for this scenario? State the reason. Read more

Steps to Solve

1. Estimate the Inertia Content of the Truck

To find the inertia content of the truck, we use the formula for inertia $I$, which is given by:

$$ I = m \cdot r^2 $$

In this scenario, the mass of the truck is 5000 tons (or $5000 \times 1000 ; kg = 5,000,000 ; kg$). The distance $r$ will depend on the radius of the wheels, but for simplification, let’s consider the inertia of the truck as its mass, since the force just moves it without rotating. Thus, we just state:

$$ I = 5,000,000 ; kg $$

2. Determine the Truck's Response Type

To determine if the truck's response is dynamic or static, we need to analyze the force being applied by the boy and the friction against the motion.

Given:

• The static friction coefficient $\mu_s = 0.3$
• The weight force $W = mg$ where $m = 5,000,000 ; kg$

Calculating the maximum static friction force:

$$ f_s = \mu_s \cdot W = 0.3 \cdot (5,000,000 ; kg \cdot 9.81 ; m/s^2) $$

Now, if the applied force $F(t)$ exceeds this maximum static friction, the truck's response becomes dynamic. Hence, calculate $F(t)$ based on the time-varying force.

3. Justify the Need for Dynamic Analysis

The justification for conducting a dynamic analysis arises from identifying whether the applied force significantly exceeds the static friction, resulting in movement and acceleration. If $F(t)$ is a time-varying force that often varies above the frictional threshold, conducting a dynamic analysis will yield insights on behavior under different conditions and help in designing systems that can withstand such variations effectively.