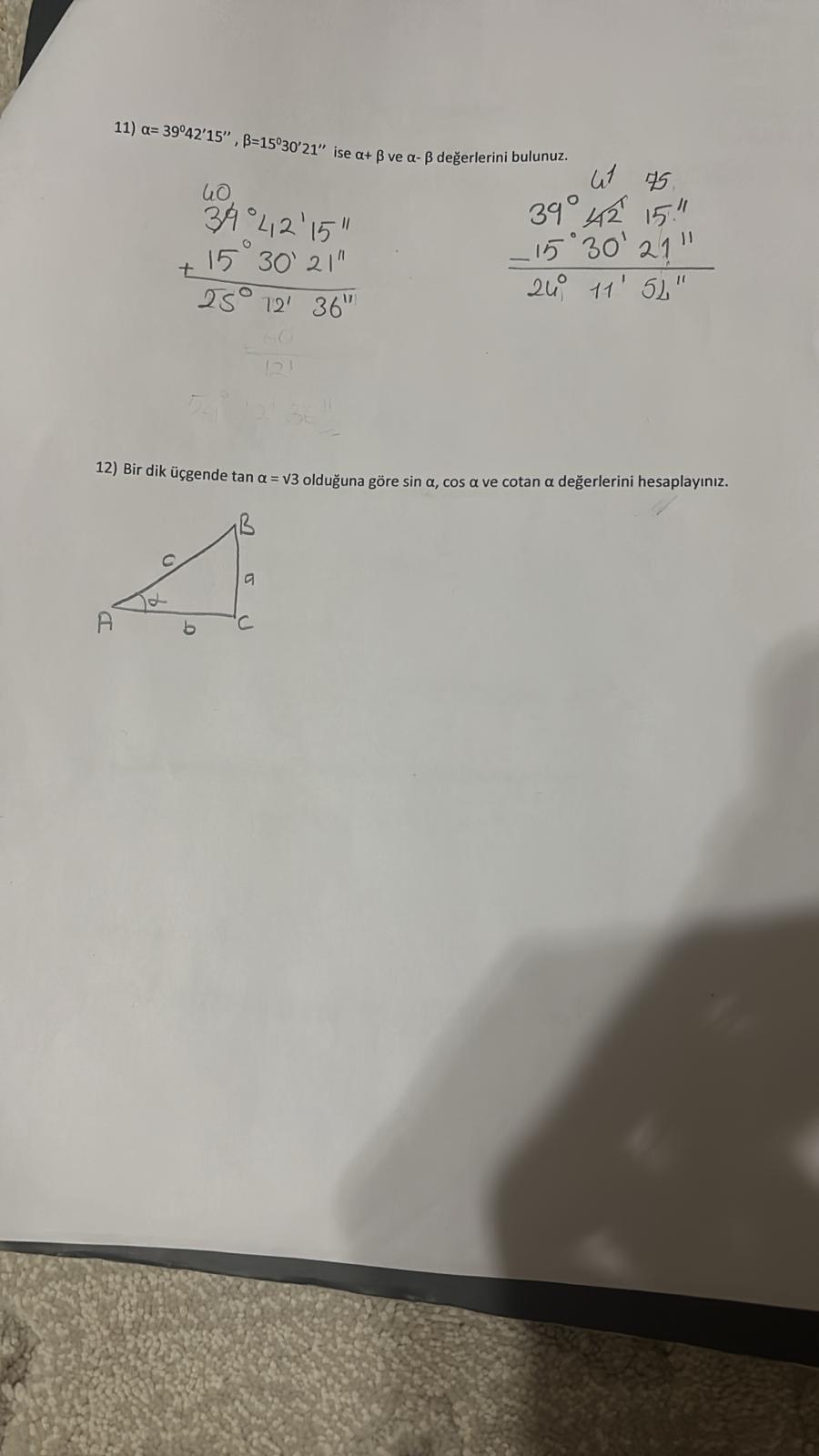
α = 39°42'15'', β = 15°30'21'' ise α + β ve α - β değerlerini bulunuz. Bir dik üçgende tan α = √3 olduğuna göre sin α, cos α ve cotan α değerlerini hesaplayınız. α = 39°42'15'', β = 15°30'21'' ise α + β ve α - β değerlerini bulunuz. Bir dik üçgende tan α = √3 olduğuna göre sin α, cos α ve cotan α değerlerini hesaplayınız.
Understand the Problem
Bu soru, verilen açıların (α ve β) toplamı ve farkı ile trigonometrik oranların (sin, cos, cotan) hesaplanmasını talep ediyor. Özellikle bir dik üçgende tan(α) değeri verilmesiyle sin(α), cos(α) ve cotan(α) hesaplamaları yapılacaktır.
Answer
$$ \sin(\alpha) = \frac{\sqrt{3}}{2}, \quad \cos(\alpha) = \frac{1}{2}, \quad \cot(\alpha) = \frac{1}{\sqrt{3}} $$
Answer for screen readers
$$ \sin(\alpha) = \frac{\sqrt{3}}{2}, \quad \cos(\alpha) = \frac{1}{2}, \quad \cot(\alpha) = \frac{1}{\sqrt{3}} $$
Steps to Solve
- Verilen bilgileri yazma
Verilen bilgiye göre tan(α) değeri $\sqrt{3}$. Bir dik üçgende tanjant, karşı kenarın komşu kenara oranıdır. Bu durumda, $$ \tan(\alpha) = \frac{a}{b} = \sqrt{3} $$
- Üçgenin oranlarını belirleme
Tan(α) değeri $\sqrt{3}$ olduğuna göre, $a = \sqrt{3}b$ şeklinde ifade edilebilir. Burada $a$ karşı kenar, $b$ komşu kenardır.
- Hipotenüs değerini bulma
Pythagor teoremini kullanarak hipotenüsü $c$ hesaplayalım: $$ c = \sqrt{a^2 + b^2} = \sqrt{(\sqrt{3}b)^2 + b^2} = \sqrt{3b^2 + b^2} = \sqrt{4b^2} = 2b $$
- Sin, Cos ve Cotan değerlerini hesaplama
Şimdi $\sin(\alpha)$, $\cos(\alpha)$ ve $\cot(\alpha)$ değerlerini hesaplayalım:
-
$\sin(\alpha)$ $$ \sin(\alpha) = \frac{a}{c} = \frac{\sqrt{3}b}{2b} = \frac{\sqrt{3}}{2} $$
-
$\cos(\alpha)$ $$ \cos(\alpha) = \frac{b}{c} = \frac{b}{2b} = \frac{1}{2} $$
-
$\cot(\alpha)$ $$ \cot(\alpha) = \frac{1}{\tan(\alpha)} = \frac{1}{\sqrt{3}} $$
$$ \sin(\alpha) = \frac{\sqrt{3}}{2}, \quad \cos(\alpha) = \frac{1}{2}, \quad \cot(\alpha) = \frac{1}{\sqrt{3}} $$
More Information
Bu sonuçlar, klasik trigonometrik oranlardır ve 60 derece için geçerlidir. Ayrıca, üçgenin oranlarıyla ilgili yapılan hesaplamalar, genel trigonometrik oranların nasıl belirleneceğini gösterir.
Tips
- Açıların oranlarını karıştırmak: Karşı ve komşu kenarları belirtirken sıklıkla hata yapılabilir. Dikkatli olunmalı.
- Pythagor teoremi uygulanırken kenar uzunluklarının doğru bir şekilde kullanılmaması.
AI-generated content may contain errors. Please verify critical information