(7/9) ÷ (8/15)
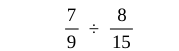
Understand the Problem
The question is presenting a mathematical equation that requires solving the division of two fractions, specifically (7/9) ÷ (8/15). We will apply the rule for dividing fractions, which is to multiply by the reciprocal.
Answer
The answer is $\frac{35}{24}$.
Answer for screen readers
The final answer is: $$ \frac{35}{24} $$
Steps to Solve
- Set up the Division of Fractions
We start with the division of the two fractions: $$ \frac{7}{9} \div \frac{8}{15} $$
- Multiply by the Reciprocal
To divide by a fraction, multiply by its reciprocal. Thus, we convert the division into multiplication: $$ \frac{7}{9} \times \frac{15}{8} $$
- Multiply the Numerators and Denominators
Now we multiply the numerators and the denominators: $$ \frac{7 \times 15}{9 \times 8} $$
- Calculate the Numerator and Denominator
This gives us:
- Numerator: $7 \times 15 = 105$
- Denominator: $9 \times 8 = 72$
Thus, we have: $$ \frac{105}{72} $$
- Simplify the Fraction
Now we need to simplify the fraction. The greatest common divisor (GCD) of 105 and 72 is 3. We divide both the numerator and the denominator by 3: $$ \frac{105 \div 3}{72 \div 3} = \frac{35}{24} $$
The final answer is: $$ \frac{35}{24} $$
More Information
The resulting fraction $\frac{35}{24}$ is an improper fraction, meaning the numerator is greater than the denominator. It can also be expressed as a mixed number which equals $1 \frac{11}{24}$.
Tips
- Forgetting to use the reciprocal: When dividing fractions, always remember to flip the second fraction.
- Miscalculating the product: Double-check multiplication of both the numerators and denominators for errors.
- Neglecting simplification: Ensure to simplify the fraction to its lowest terms.
AI-generated content may contain errors. Please verify critical information