77. Simplify \(\cos^2 A(1 + \tan^2 A)\) 78. What is the value of \(\tan 30^\circ \)?
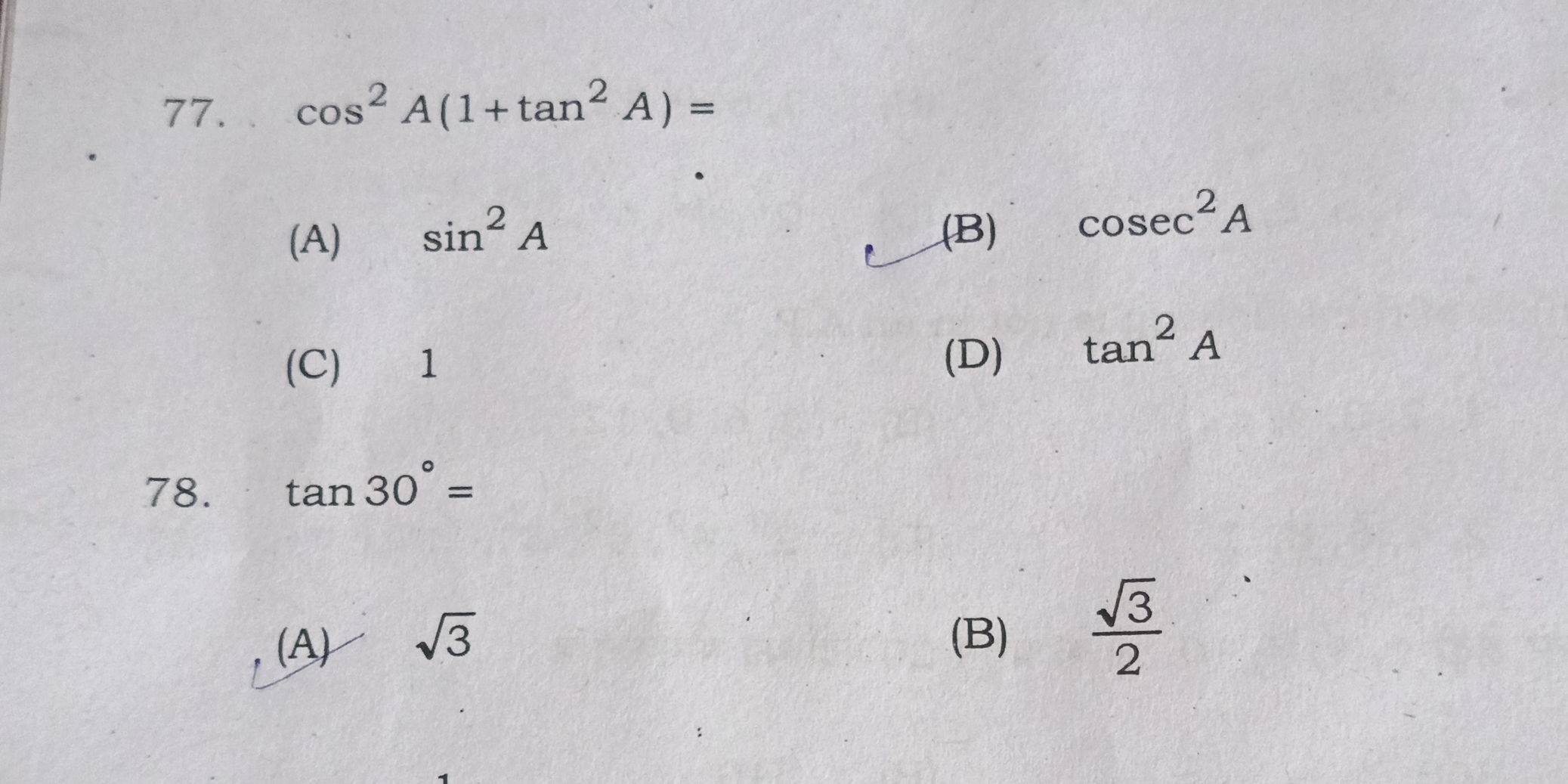
Understand the Problem
The image presents two trigonometry questions. The first asks to simplify (\cos^2 A(1 + \tan^2 A)). The second question is asking us to identify the value of (\tan 30^\circ ).
Answer
77. 1 78. $\frac{\sqrt{3}}{3}$
Answer for screen readers
- (C) 1
- None of the options are appropriate, the correct answer is $\frac{\sqrt{3}}{3}$
Steps to Solve
-
Simplify using trigonometric identity We know that $1 + \tan^2 A = \sec^2 A$. So, we can substitute this into the expression: $\cos^2 A (1 + \tan^2 A) = \cos^2 A (\sec^2 A)$
-
Further simplification using reciprocal identity Since $\sec A = \frac{1}{\cos A}$, then $\sec^2 A = \frac{1}{\cos^2 A}$. Substituting this, we get: $\cos^2 A (\sec^2 A) = \cos^2 A \cdot \frac{1}{\cos^2 A}$
-
Final simplification $\cos^2 A \cdot \frac{1}{\cos^2 A} = 1$
-
Find $\tan 30^\circ$ value The value of $\tan 30^\circ$ is a standard trigonometric value which is $\frac{1}{\sqrt{3}}$ which can also be written as $\frac{\sqrt{3}}{3}$. We observe that the given options do not include $\frac{\sqrt{3}}{3}$ but they include $\sqrt{3}$. This is incorrect, the correct answer is $\frac{\sqrt{3}}{3}$
- (C) 1
- None of the options are appropriate, the correct answer is $\frac{\sqrt{3}}{3}$
More Information
- The first question uses the trigonometric identity $1 + \tan^2 A = \sec^2 A$ and the reciprocal indentity to find the answer
- $ \tan 30^\circ = \frac{\sqrt{3}}{3}$
Tips
- For question 77, students may not remember the trigonometric identity $1 + \tan^2 A = \sec^2 A$.
- For question 78, students may confuse the value of $\tan 30^\circ$ with other standard values like $\tan 45^\circ$ or $\tan 60^\circ$.
- Ensure you know the values for all of the basic trig functions
AI-generated content may contain errors. Please verify critical information