5x - 7y = -19; -7x + 4y = -14

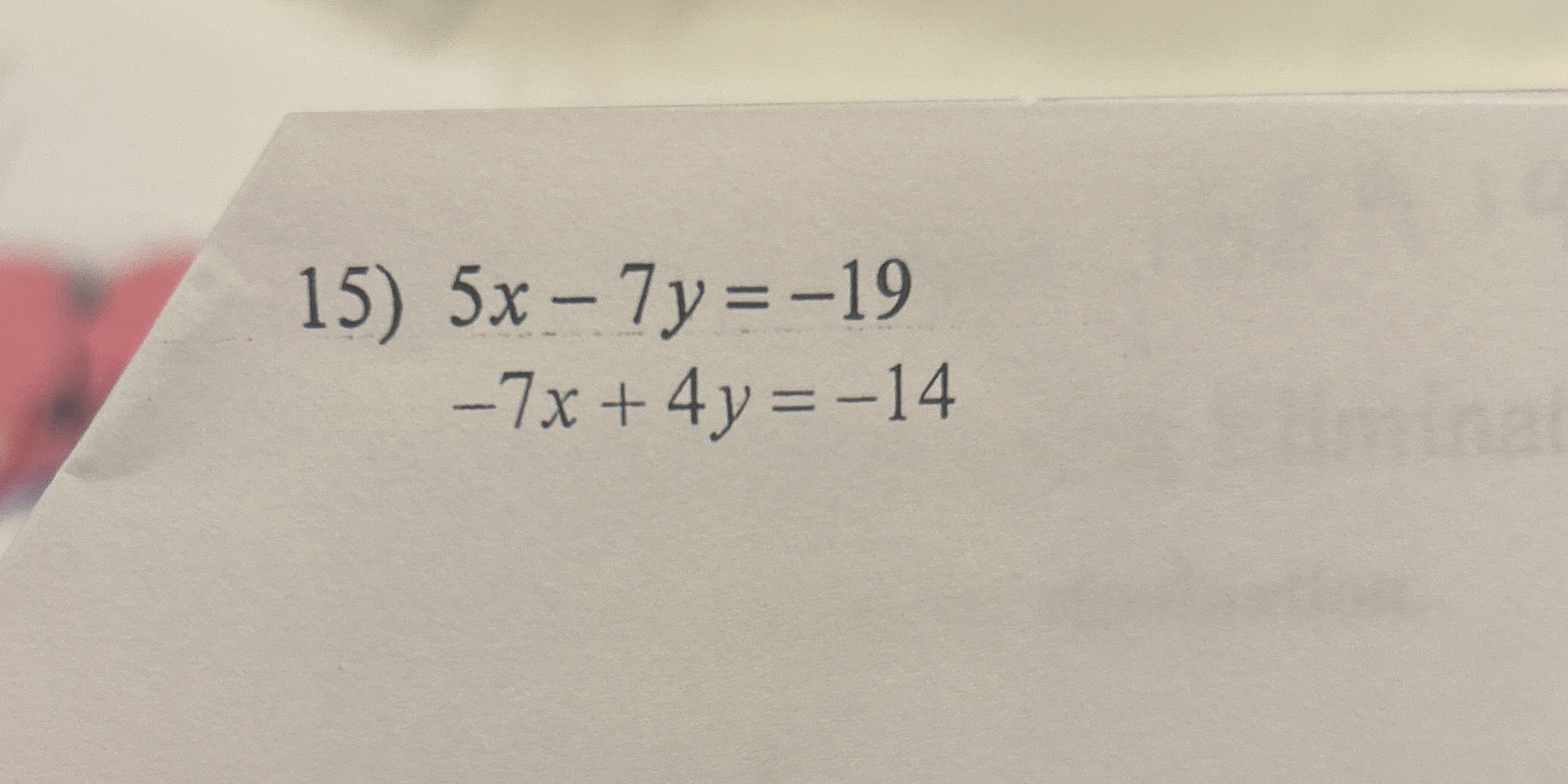
Understand the Problem

The question provides a system of equations and asks for a solution, likely through methods such as substitution or elimination.

Answer

The solution is $ x = 6 $ and $ y = 7 $.

Steps to Solve

Rearranging One Equation for Substitution

Select the first equation and rearrange it to solve for $y$:

Starting with the equation:

$$ 5x - 7y = -19 $$

Isolate $y$:

$$ -7y = -19 - 5x $$

Divide by -7:

$$ y = \frac{5x + 19}{7} $$

Substituting into the Second Equation

Now, substitute the expression for $y$ into the second equation:

The second equation is:

$$ -7x + 4y = -14 $$

Substituting $y$ from the first equation gives:

$$ -7x + 4\left(\frac{5x + 19}{7}\right) = -14 $$

Clearing the Fraction

To eliminate the fraction, multiply the entire equation by 7:

$$ -49x + 4(5x + 19) = -98 $$

Distributing the 4:

$$ -49x + 20x + 76 = -98 $$

Combining Like Terms

Combine the $x$ terms:

$$ -29x + 76 = -98 $$

Isolating x

Subtract 76 from both sides:

$$ -29x = -174 $$

Divide by -29:

$$ x = \frac{174}{29} = 6 $$

Substituting back to find y

Now substitute $x = 6$ back into the equation we derived for $y$:

$$ y = \frac{5(6) + 19}{7} $$

Calculate:

$$ y = \frac{30 + 19}{7} = \frac{49}{7} = 7 $$

The solution to the system of equations is ( x = 6 ) and ( y = 7 ).

More Information

This is a linear system of equations, and the solution shows the point at which both lines represented by the equations intersect. This point can be confirmed by substituting ( x ) and ( y ) back into the original equations.

Tips

Failing to distribute correctly when substituting ( y ) into the second equation.
Forgetting to simplify fractions before solving for ( x ) or ( y ).
Confusing the signs when isolating variables.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!