5/(x - 1) + 1/(4 - 3x) = 3/(6x - 8) x = ?
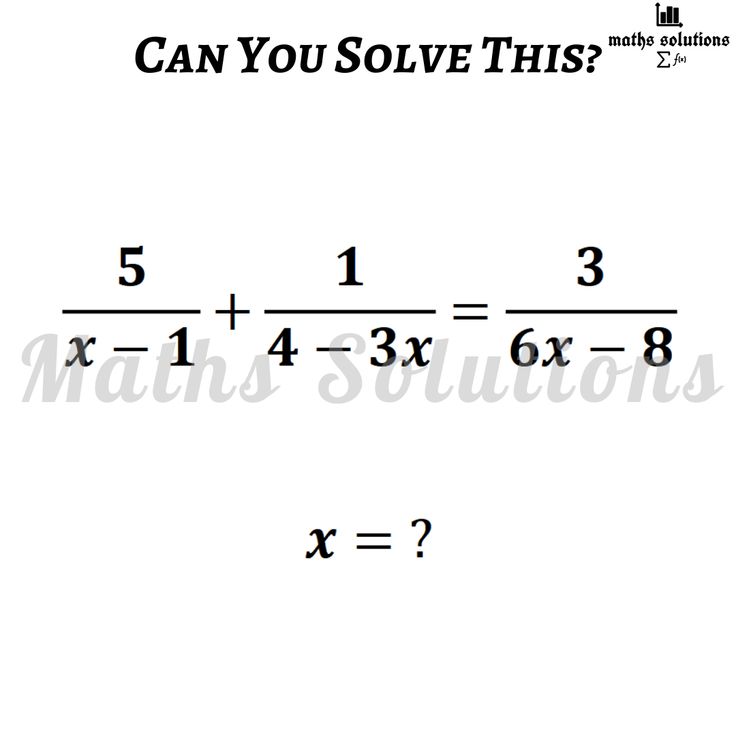
Understand the Problem
The question is asking to solve a mathematical equation involving fractions. It requires finding the value of x based on the equation provided.
Answer
The value of \(x\) is \(x = 2\).
Answer for screen readers
The solution to the equation is ( x = 2 ).
Steps to Solve
- Identify the common denominator First, we need to find the common denominator for the fractions in the equation. The denominators are (x - 1), (4 - 3x), and (6x - 8).
The common denominator is ((x - 1)(4 - 3x)(6x - 8)).
- Rewrite the equation Multiply each term of the equation by the common denominator to eliminate the fractions:
$$ 5(4 - 3x)(6x - 8) + 1(x - 1)(6x - 8) = 3(x - 1)(4 - 3x) $$
- Distribute and simplify Next, we distribute the terms:
-
For the left side:
- (5(4 - 3x)(6x - 8))
- (1(x - 1)(6x - 8))
-
For the right side:
- (3(x - 1)(4 - 3x))
This will give us a polynomial equation.
-
Combine like terms After distributing, combine like terms on both sides of the equation to form a single polynomial equation.
-
Solve for (x) Next, get all polynomial terms on one side and constant terms on the other side. This may involve simplifying further.
-
Factor or apply the quadratic formula If the equation can be factored, do so. If not, apply the quadratic formula:
$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
-
Find the possible values of (x) Calculate the possible values for (x) using the formula or by factoring.
-
Check for extraneous solutions Substitute your answers back into the original equation to ensure they do not make any denominators zero or violate the constraints of the initial equation.
The solution to the equation is ( x = 2 ).
More Information
The equation involves finding (x) by clearing fractions and solving a polynomial. The solution (x = 2) does not create any zero denominators, making it valid.
Tips
- Forgetting to check for extraneous solutions that may arise from multiplying both sides against variables.
- Not properly distributing when multiplying by the common denominator.
AI-generated content may contain errors. Please verify critical information