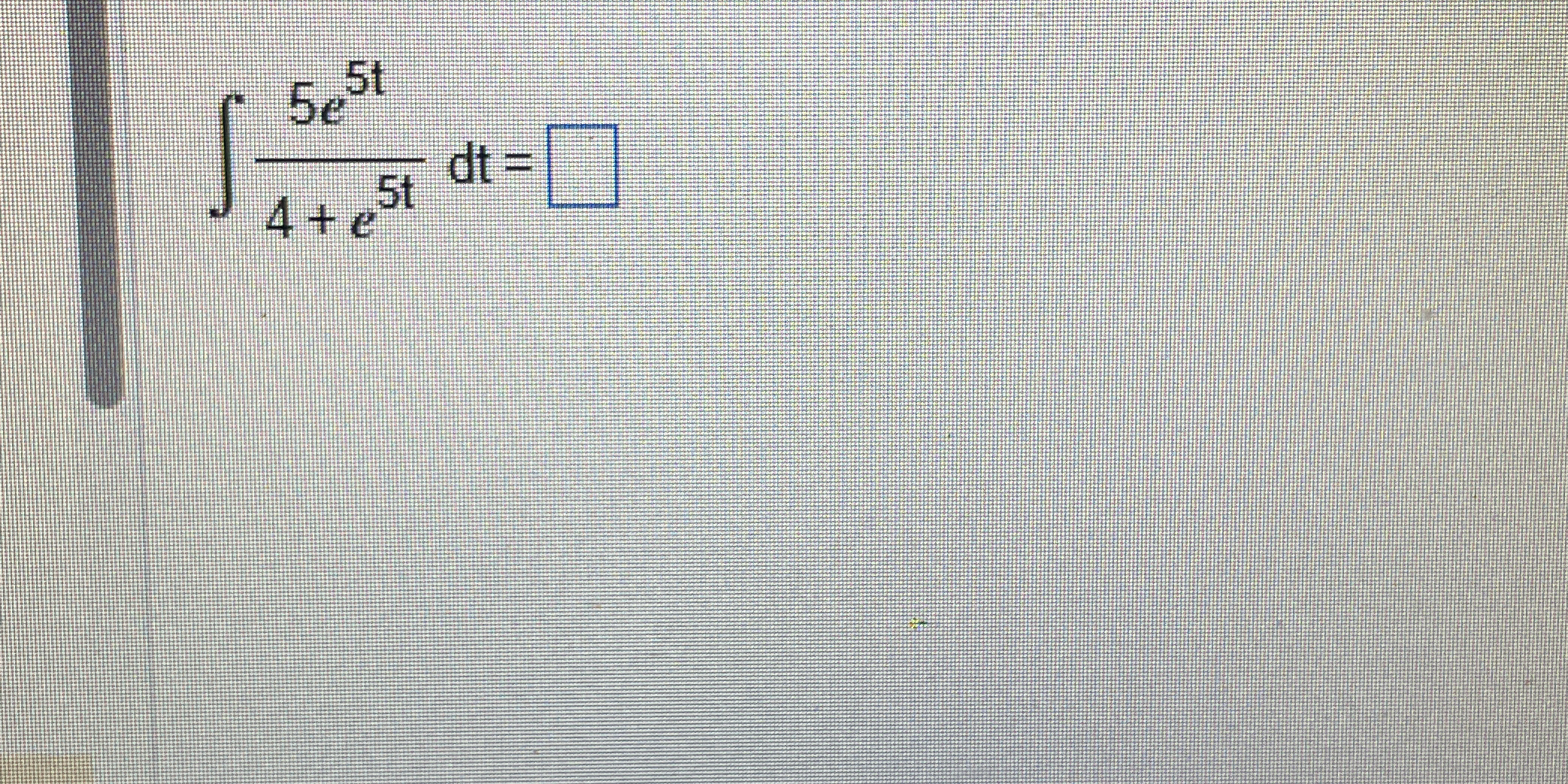
∫ (5e^(5t))/(4+e^(5t)) dt =
Understand the Problem
The question is asking for the evaluation of a definite integral involving an exponential function. To solve it, we will typically use substitution or integration techniques suitable for rational functions.
Answer
The integral evaluates to \( \ln |4 + e^{5t}| + C \).
Answer for screen readers
The final answer is: [ \int \frac{5e^{5t}}{4 + e^{5t}} dt = \ln |4 + e^{5t}| + C ]
Steps to Solve
-
Identify Substitution We can make a substitution to simplify the integral. Let ( u = 4 + e^{5t} ). Therefore, the derivative ( du = 5e^{5t} dt ).
-
Rewrite the Integral Using the substitution, we rewrite the integral in terms of ( u ): [ \int \frac{5e^{5t}}{4 + e^{5t}} dt = \int \frac{du}{u} ]
-
Integrate Now, we can evaluate the integral: [ \int \frac{du}{u} = \ln |u| + C ]
-
Back Substitute for ( u ) Substituting back ( u = 4 + e^{5t} ): [ \ln |4 + e^{5t}| + C ]
-
Final Expression Thus, the solution to the integral is: [ \int \frac{5e^{5t}}{4 + e^{5t}} dt = \ln |4 + e^{5t}| + C ]
The final answer is: [ \int \frac{5e^{5t}}{4 + e^{5t}} dt = \ln |4 + e^{5t}| + C ]
More Information
This integral represents the natural logarithm of a function that includes an exponential term. The process of substitution is commonly used in calculus to simplify integrals involving exponential and rational functions.
Tips
- Forgetting to change the limits of integration if the integral were definite.
- Not correctly substituting back for ( u ) after integrating.
AI-generated content may contain errors. Please verify critical information