∫ -5cos(πx) dx
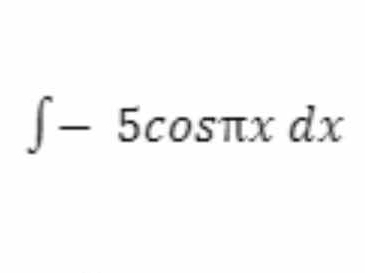
Understand the Problem
The question is asking us to evaluate the integral of the function -5cos(πx) with respect to x. This involves applying integral calculus techniques to find the antiderivative of the function.
Answer
$$ -\frac{5}{\pi} \sin(\pi x) + C $$
Answer for screen readers
The final answer is: $$ -\frac{5}{\pi} \sin(\pi x) + C $$
Steps to Solve
-
Identify the integral to evaluate We need to evaluate the integral $$ \int -5\cos(\pi x) , dx $$.
-
Factor out the constant Since we have a constant multiplier in the integrand, we can factor it out of the integral. This gives us: $$ -5 \int \cos(\pi x) , dx $$
-
Find the antiderivative of cos(πx) The antiderivative of $\cos(kx)$ is $\frac{1}{k}\sin(kx)$, where $k$ is a constant. Here, $k = \pi$, so: $$ \int \cos(\pi x) , dx = \frac{1}{\pi} \sin(\pi x) $$
-
Combine the constants and finalize the expression Now we can substitute back into the previous expression: $$ -5 \cdot \frac{1}{\pi} \sin(\pi x) + C $$
-
Write the final result Combining everything, the evaluated integral is: $$ -\frac{5}{\pi} \sin(\pi x) + C $$
The final answer is: $$ -\frac{5}{\pi} \sin(\pi x) + C $$
More Information
This result represents the antiderivative of the function $-5\cos(\pi x)$. The constant $C$ is included because when finding antiderivatives, there can be infinitely many solutions differing by a constant.
Tips
- Forgetting to include the constant of integration $C$.
- Misapplying the formula for the antiderivative of cosine functions, particularly the factor of $\frac{1}{k}$.
AI-generated content may contain errors. Please verify critical information